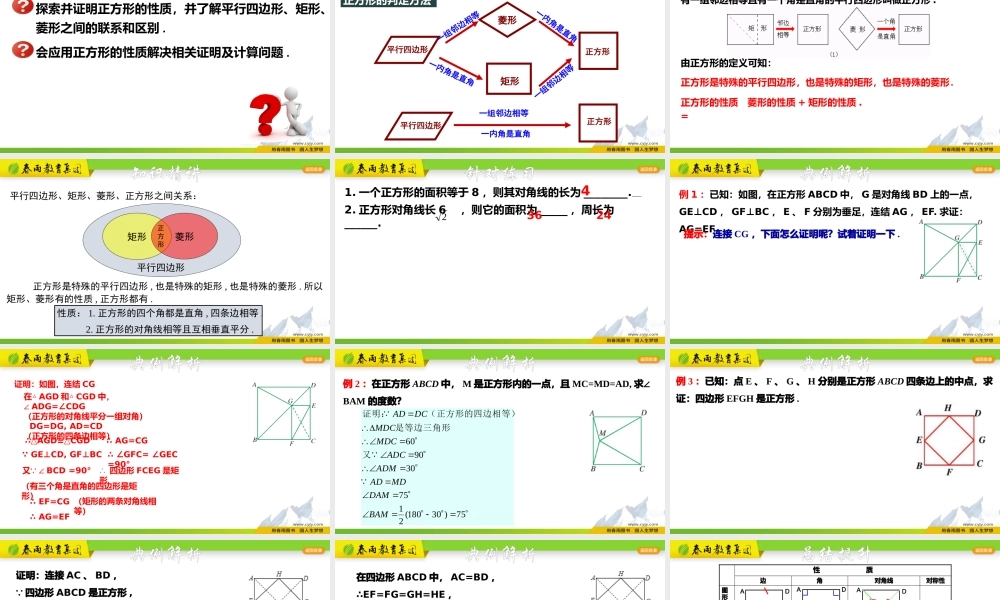
学习目标探索并证明正方形的性质,并了解平行四边形、矩形、菱形之间的联系和区别.会应用正方形的性质解决相关证明及计算问题.正方形的判定方法平行四边形正方形矩形菱形一组邻边相等一组邻边相等一内角是直角一内角是直角平行四边形正方形一组邻边相等一内角是直角复习回顾由正方形的定义可知:有一组邻边相等且有一个角是直角的平行四边形叫做正方形.正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.正方形的性质=菱形的性质+矩形的性质.知识精讲矩形菱形正方形平行四边形正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.平行四边形、矩形、菱形、正方形之间关系:性质:1.正方形的四个角都是直角,四条边相等.2.正方形的对角线相等且互相垂直平分.知识精讲1.一个正方形的面积等于8,则其对角线的长为________.42.正方形对角线长6,则它的面积为_____,周长为______.23624针对练习例1:已知:如图,在正方形ABCD中,G是对角线BD上的一点,GE⊥CD,GF⊥BC,E、F分别为垂足,连结AG,EF.求证:AG=EF提示:连接CG,下面怎么证明呢?试着证明一下.典例解析 GE⊥CD,GF⊥BC∴∠GFC=∠GEC=90°(有三个角是直角的四边形是矩形)又 ∠BCD=90°∴AG=CG∴四边形FCEG是矩形证明:如图,连结CG在△AGD和△CGD中,∠ADG=∠CDG(正方形的对角线平分一组对角)DG=DG,AD=CD(正方形的四条边相等)∴△AGD≌△CGD∴AG=EF∴EF=CG(矩形的两条对角线相等)典例解析例2:在正方形ABCD中,M是正方形内的一点,且MC=MD=AD,求∠BAM的度数?典例解析75)30180(2175309060BAMDAMMDADADMADCMDCMDCDCAD又是等边三角形(正方形的四边相等)证明:例3:已知:点E、F、G、H分别是正方形ABCD四条边上的中点,求证:四边形EFGH是正方形.典例解析证明:连接AC、BD, 四边形ABCD是正方形,∴AC=BD,AC⊥BD,在△ABC中,F.G分别是AB、BC的中点,故可得:FG=AC,同理EH=AC,GH=BD,EF=BD,21212121典例解析在四边形ABCD中,AC=BD,∴EF=FG=GH=HE,∴四边形EFGH是菱形。在△ABD中,E.H分别是AD、CD的中点,则EH∥AC,同理GH∥BD,又 AC⊥BD,∴EH⊥HG,∴四边形EFGH是正方形.典例解析性质边角对角线对称性图形语言文字语言符号语言ACD\BACDBACDB\\\∟∟∟∟O\\\\∟对边平行,四条边都相等四个角都是直角对角线互相垂直平分且相等,每条对角线平分一组对角 四边形ABCD...