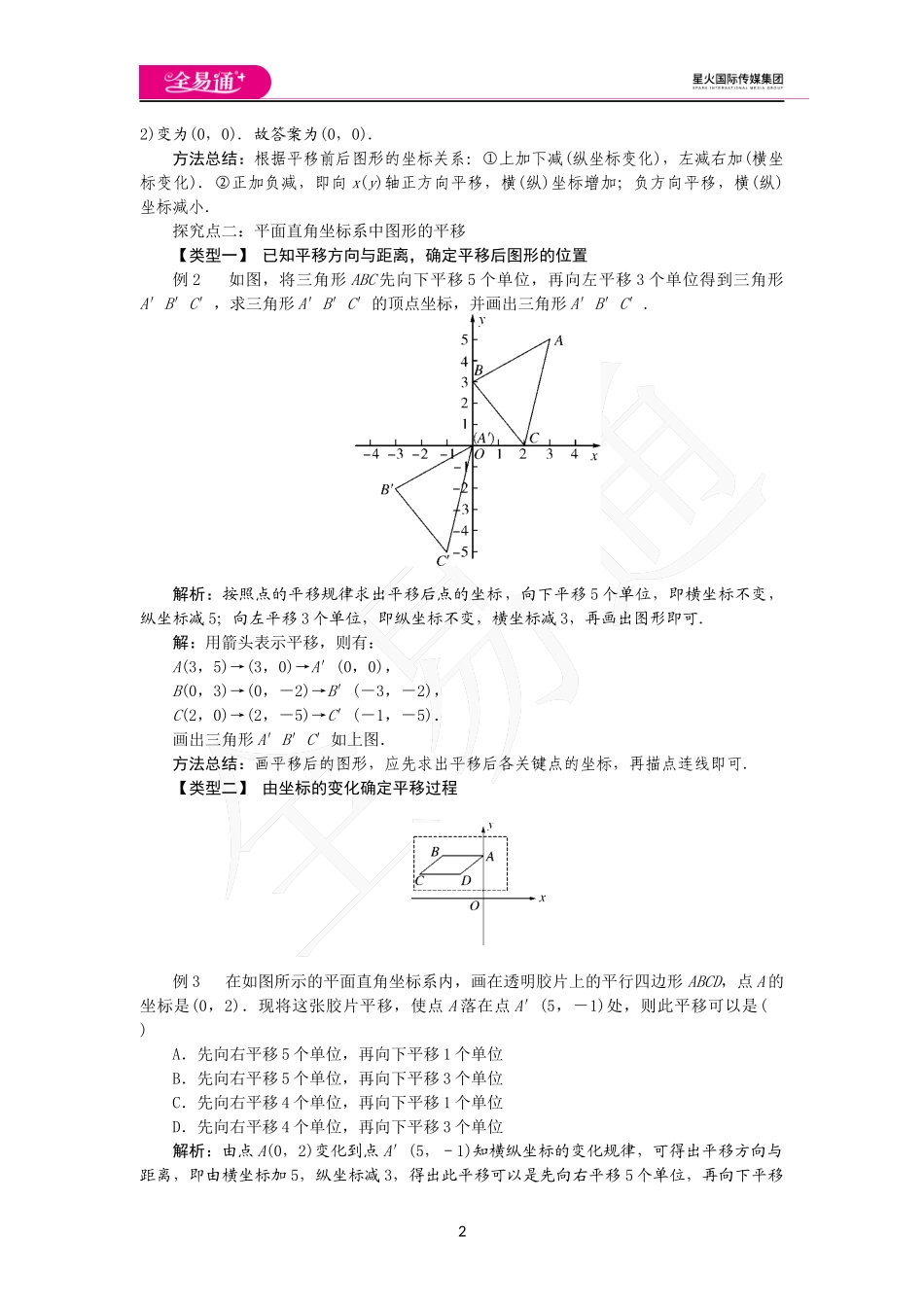
111.2图形在坐标系中的平移教学目标【知识与能力】1.能在直角坐标系中用坐标的方法研究图形的平移变换,掌握图形在平移过程中各点的变化规律,理解图形在平面直角坐标系上的平移实质是点坐标的对应变换。2.运用点的坐标的变化规律来进行简单的平移作图。【过程与方法】本节课的教学过程中,无论是从情境中引入,还是对新知的探究及拓展,要始终调动学生学习的积极性,使学生看到平面直角坐标系是数与形之间的桥梁,感受到代数与几何的相互转化。【情感态度价值观】经历观察、分析、抽象、归纳等过程,让学生体验数学活动充满着探索性与创造性,激发学生的学习兴趣,感受数学在生活中的应用,增强学生的数学应用意识,让学生认识数学与人类生活的密切联系,提高他们学习数学的兴趣。教学重难点【教学重点】认识直角坐标系,感受点在坐标系中的平移过成及其应用。【教学难点】根据图形的平移过程,探索、归纳出坐标的变化规律。课前准备课件、教具等。教学过程一、情境导入同学们会下棋吗?棋子的移动,什么在变,什么不变?那么在棋盘上推动棋子是否可以看成图形在平面上的平移?二、合作探究探究点一:平面直角坐标系中点的平移例1将点(1,2)向左平移1个单位,再向下平移2个单位后得到对应点的坐标是________.解析:向左平移1个单位,横坐标减1,向下平移2个单位,纵坐标减2,于是点(1,22)变为(0,0).故答案为(0,0).方法总结:根据平移前后图形的坐标关系:①上加下减(纵坐标变化),左减右加(横坐标变化).②正加负减,即向x(y)轴正方向平移,横(纵)坐标增加;负方向平移,横(纵)坐标减小.探究点二:平面直角坐标系中图形的平移【类型一】已知平移方向与距离,确定平移后图形的位置例2如图,将三角形ABC先向下平移5个单位,再向左平移3个单位得到三角形A′B′C′,求三角形A′B′C′的顶点坐标,并画出三角形A′B′C′.解析:按照点的平移规律求出平移后点的坐标,向下平移5个单位,即横坐标不变,纵坐标减5;向左平移3个单位,即纵坐标不变,横坐标减3,再画出图形即可.解:用箭头表示平移,则有:A(3,5)→(3,0)→A′(0,0),B(0,3)→(0,-2)→B′(-3,-2),C(2,0)→(2,-5)→C′(-1,-5).画出三角形A′B′C′如上图.方法总结:画平移后的图形,应先求出平移后各关键点的坐标,再描点连线即可.【类型二】由坐标的变化确定平移过程例3在如图所示的平面直角坐标系内,画在透明胶片上的平行四边形ABCD,点A的坐标是(0,2).现将...