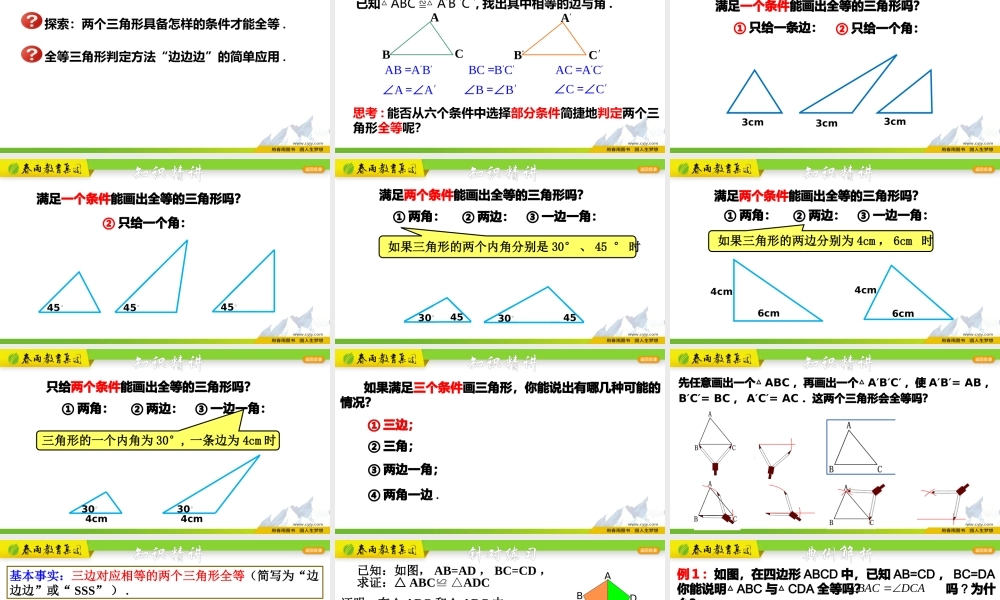
学习目标探索:两个三角形具备怎样的条件才能全等.全等三角形判定方法“边边边”的简单应用.知识精讲∠A=∠A′AB=A′B′已知△ABC≌△A′B′C′,找出其中相等的边与角.思考:能否从六个条件中选择部分条件简捷地判定两个三角形全等呢?ABCA′B′C′∠B=∠B′BC=B′C′∠C=∠C′AC=A′C′知识精讲满足一个条件能画出全等的三角形吗?3cm3cm3cm①只给一条边:②只给一个角:知识精讲满足一个条件能画出全等的三角形吗?45◦45◦45◦②只给一个角:知识精讲满足两个条件能画出全等的三角形吗?①两角:②两边:30◦45◦30◦45◦③一边一角:如果三角形的两个内角分别是30°、45°时知识精讲满足两个条件能画出全等的三角形吗?①两角:②两边:③一边一角:如果三角形的两边分别为4cm,6cm时6cm6cm4cm4cm知识精讲只给两个条件能画出全等的三角形吗?①两角:②两边:③一边一角:三角形的一个内角为30°,一条边为4cm时4cm4cm30◦30◦知识精讲如果满足三个条件画三角形,你能说出有哪几种可能的情况?①三边;②三角;③两边一角;④两角一边.①三边;知识精讲先任意画出一个△ABC,再画出一个△A′B′C′,使A′B′=AB,B′C′=BC,A′C′=AC.这两个三角形会全等吗?知识精讲基本事实:三边对应相等的两个三角形全等(简写为“边边边”或“SSS”).用数学符号语言表述:在△ABC和△DEF中∴△ABC≌△DEF(SSS)AB=DEBC=EFCA=FDABCDEF文字语言文字语言符号语言符号语言图形语言图形语言针对练习已知:如图,AB=AD,BC=CD,求证:△ABCADC≌△ABCDAC=AB=≌∴△ABC(SSS)证明:在△ABC和△ADC中(已知)()(公共边)BC=我们把判断两个三角形全等的推理过程,叫做证明三角形全等典例解析例1:如图,在四边形ABCD中,已知AB=CD,BC=DA你能说明△ABC与△CDA全等吗?吗?为什么?DBAC解:在△ABC与△CDA中, ∴△ABCCDA≌△(SSS)BC=DAAB=CDAC=CA(公共边)(已知)(已知)BACDCA∴BACDCA(全等三角形的对应角相等)①准备条件:证全等时要用的条件要先证好;②指明范围:写出在哪两个三角形中;③摆齐根据:摆出三个条件用大括号括起来;④写出结论:写出全等结论.证明的书写步骤:归纳总结证明:因为BE=CF,所以BE+EC=CF+EC,即BC=EF.在△ABC和△DEF中,AB=DE,BC=EF,AC=DF,所以△ABC≌△DEF(SSS).如图,已知点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF.求证:(1)△ABC≌△DEF;针对练习(2)ABDE.∥解:由(1)知△ABC≌...