1.3.1 平行线的判定（一）.pptxVIP免费

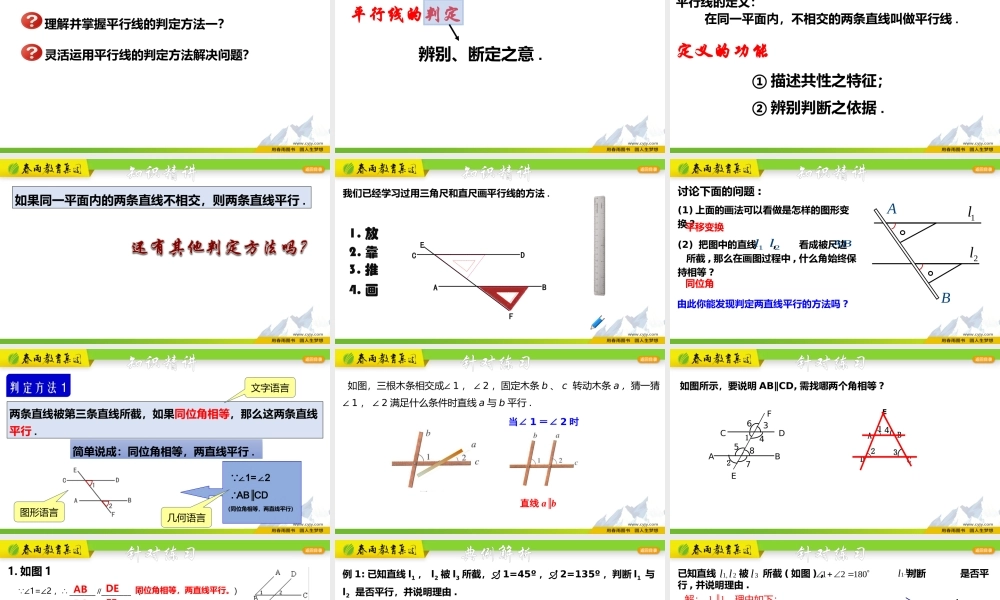
学习目标理解并掌握平行线的判定方法一？灵活运用平行线的判定方法解决问题？知识链接平行线的判定辨别、断定之意.知识链接定义的功能①描述共性之特征；②辨别判断之依据.平行线的定义：在同一平面内，不相交的两条直线叫做平行线.如果同一平面内的两条直线不相交，则两条直线平行.知识精讲知识精讲我们已经学习过用三角尺和直尺画平行线的方法.CEABFD1.放2.靠3.推4.画讨论下面的问题:(1)上面的画法可以看做是怎样的图形变换?1l2lAB(2)把图中的直线,看成被尺边所截,那么在画图过程中,什么角始终保持相等?1l2lAB平移变换同位角由此你能发现判定两直线平行的方法吗?知识精讲判定方法1两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行.简单说成：同位角相等，两直线平行. ∠1=2∠∴ABCD∥（同位角相等，两直线平行）文字语言几何语言图形语言知识精讲如图，三根木条相交成∠1，∠2，固定木条b、c转动木条a,猜一猜∠1，∠2满足什么条件时直线a与b平行.当∠1＝∠2时直线a∥b针对练习E12345678ABCDF如图所示，要说明AB∥CD,需找哪两个角相等?ADCB123E4针对练习 ∠1=∠2，∴_______∥________（） ∠2=∠3，∴_______∥________（）1.如图1 ∠B=∠_______，∴AB∥CD（） ∠BGC=∠_______，∴CD∥EF（） AB∥CD，CD∥EF，∴AB∥_______（）2.如图2图1图2针对练习同位角相等，两直线平行。同位角相等，两直线平行。ABDEBCEFCGFFEF同位角相等，两直线平行。同位角相等，两直线平行。如果两条直线都与第三条直线平行，那么这两条直线也互相平行。例1:已知直线l1，l2被l3所截，1=45º，2=135º，判断l1与l2是否平行，并说明理由.321l1l2l3解：l1l∥2．理由如下：由已知，得∠2+3=180°∠∴∠3=180°－∠2=180°－135°=45°又 ∠1=45°∴∠1=3∠∴l1l∥2（同位角相等，两直线平行）典例解析已知直线被所截(如图),判断是否平行,并说明理由.2,1ll3l21ll与l3l2l1123l3l2l11212180针对练习解：l1l∥2．理由如下：由已知，得∠1+2=180°∠ ∠2+3=180°∠∴∠1=3∠（同角的补角相等）∴l1l∥2（同位角相等，两直线平行）已知直线被所截(如图),判断是否平行,并说明理由.2,1ll3l21ll与针对练习解：l1l∥2．理由如下：由已知，得∠1=2∠ ∠2=3∠（对顶角相等）∴∠1=3∠（等量代换）∴l1l∥2（同位角相等，两直线平行）12l3l2l121l3l2l1231例2：已知：AB⊥EF,CD⊥EF,E,F分别为垂足，直线AB与CD平行吗？请说明理由.∴AB∥CD....