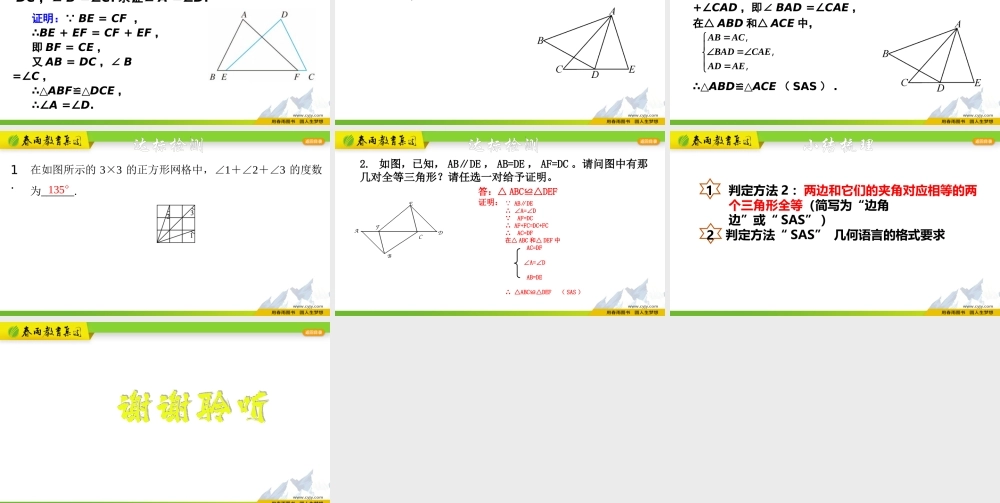
学习目标已知三角形的两边和一角,有哪几种可能的情况?已知两个三角形的两边和一角分别相等,能否判断两个三角形全等?复习回顾基本事实:三边对应相等的两个三角形全等(简写为“边边边”或“SSS”).回忆知识精讲如果已知一个三角形的两边及一角,那么有几种可能的情况呢?每种情况下得到的三角形都全等吗?1、边角边;2、边边角;知识精讲A′DE现象:两个三角形放在一起能完全重合.说明:这两个三角形全等.画法:(1)画∠DA′E=∠A;(2)在射线A′D上截取A′B′=AB,在射线A′E上截取A′C′=AC;(3)连接B′C′.B′C′知识精讲基本事实:两边和它们的夹角分别相等的两个三角形全等(简写为“边角边”或“SAS”).用数学符号语言表述:在△ABC和△A′B′C′中∴△ABCA′B′C′≌△(SAS).AB=A′B′∠A=A′∠AC=A′C′文字语言文字语言符号语言符号语言图形语言图形语言针对训练下列图形中有没有全等三角形,并说明全等的理由.甲8cm9cm丙8cm9cm8cm9cm乙30°30°30°相等,根据边角边定理,△BAD≌△BAC,∴BD=BC。如图,两车从南北方向的路段AB的A端出发,分别向东、向西行进相同的距离,到达C,D两地.此时C,D到B的距离相等吗?为什么?巩固训练如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个不经过池塘可以直接到达点A和B的点C,连接AC并延长至D,使CD=CA,连接BC并延长至E,使CE=CB,连接ED,那么量出DE的长就是A,B的距离.为什么?ABEDC实际应用如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个不经过池塘可以直接到达点A和B的点C,连接AC并延长至D,使CD=CA,连接BC并延长至E,使CE=CB,连接ED,那么量出DE的长就是A,B的距离.为什么?ABEDCAC=DC(已知),∠1=∠2(对顶角相等),BC=EC(已知),证明:在△ABC和△DEC中,∴△ABC≌△DEC(SAS).∴AB=DE(全等三角形的对应边相等).实际应用拓展提升证明: BE=CF,∴BE+EF=CF+EF,即BF=CE,又AB=DC,∠B=∠C,∴△ABF≌△DCE,∴∠A=∠D.如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C.求证∠A=∠D.已知:如图AB=AC,AD=AE,∠BAC=∠DAE,求证:△ABD≌△ACE.拓展提升证明: ∠BAC=∠DAE,∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,在△ABD和△ACE中,∴△ABD≌△ACE(SAS).ABACBADCAEADAE,,,拓展提升达标检测16.在如图所示的3×3的正方形网格中,∠1+∠2+∠3的度数为______.135°1.证明: AB∥DE∴∠A=∠D AF=DC∴AF+F...