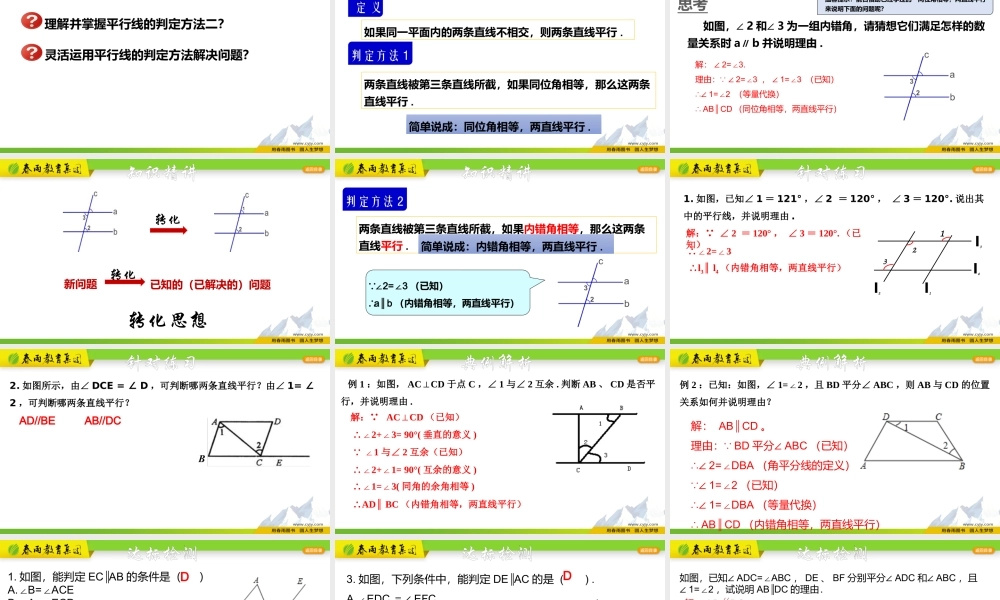
理解并掌握平行线的判定方法二?灵活运用平行线的判定方法解决问题?学习目标复习回顾如果同一平面内的两条直线不相交,则两条直线平行.判定方法1两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.定义简单说成:同位角相等,两直线平行.知识精讲思考如图,∠2和∠3为一组内错角,请猜想它们满足怎样的数量关系时a∥b并说明理由.温馨提示:能否借助已经学过的“同位角相等,两直线平行”来说明下面的问题呢?解:∠2=3.∠理由: ∠2=3∠,∠1=3∠(已知)∴∠1=2∠(等量代换)∴AB∥CD(同位角相等,两直线平行)新问题已知的(已解决的)问题转化转化思想1转化知识精讲知识精讲判定方法2两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单说成:内错角相等,两直线平行. ∠2=3∠(已知)∴a∥b(内错角相等,两直线平行)1.如图,已知∠1=121°,∠2=120°,∠3=120°.说出其中的平行线,并说明理由.123l2l1l3l4针对练习解: ∠2=120°,∠3=120°.(已知)∴∠2=3∠∴l3l∥4(内错角相等,两直线平行)2.如图所示,由∠DCE=∠D,可判断哪两条直线平行?由∠1=∠2,可判断哪两条直线平行?AD//BEAB//DC针对练习解: ACCD⊥(已知)∴∠2+3=90°(∠垂直的意义)∴ADBC∥(内错角相等,两直线平行) ∠1与∠2互余(已知)∴∠2+1=90°(∠互余的意义)∴∠1=3(∠同角的余角相等)例1:如图,ACCD⊥于点C,∠1与∠2互余.判断AB、CD是否平行,并说明理由.典例解析典例解析例2:已知:如图,∠1=2∠,且BD平分∠ABC,则AB与CD的位置关系如何并说明理由?解:AB∥CD。理由: BD平分∠ABC(已知)∴∠2=DBA∠(角平分线的定义) ∠1=2∠(已知)∴∠1=DBA∠(等量代换)∴AB∥CD(内错角相等,两直线平行)达标检测1.如图,能判定EC∥AB的条件是()A.B=ACE∠∠B.A=ECD∠∠C.B=ACB∠∠D.A=ACE∠∠2.如图,下列条件中,能判定AB∥CD的是()A.2∠=∠4B.1∠=∠3C.C∠=∠5D.A=4∠∠DB达标检测3.如图,下列条件中,能判定DEAC∥的是().A.EDC∠=∠EFCB.AFE∠=∠ACDC.1∠=∠2D.3∠=∠4D达标检测如图,已知∠ADC=ABC∠,DE、BF分别平分∠ADC和∠ABC,且∠1=2∠,试说明AB∥DC的理由.达标检测如图,ABBC⊥,BCCD⊥,∠1=2∠.试判断BE与CF的关系,并说明理由.解:BE∥CF.理由如下: AB⊥BC,BC⊥CD(已知),∴∠ABC=∠BCD=90°(垂直的定义)即∠1+∠EBC=∠2+∠BCF(等量关系);又 ∠1=∠2(已知),∴∠EBC...