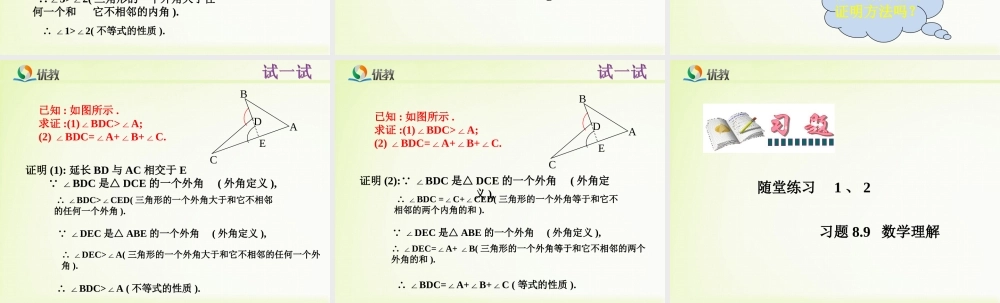
8.6三角形内角和定理(3)三角形内角和定理:三角形三个内角的和等于180°。推论1:三角形的一个外角等于和它不相邻的两个内角的和.推论2:三角形的一个外角大于任何一个和它不相邻的内角.推论3:直角三角形的两锐角互余.已知:国旗上的正五角星形如图所示.求:A+B+C+D+E∠∠∠∠∠的度数.解:1∵∠是△BDF的一个外角(外角的定义),∴∠1=B+D(∠∠三角形的一个外角等于和它不相邻的两个内角的和).∴∠2=C+E(∠∠三角形的一个外角等于和它不相邻的两个内角的和).又∵∠A+1+2=180°(∠∠三角形内角和定理).又∵∠2是△EHC的一个外角(外角的定义),ABCDEF1H2∴∠A+B+C+D+E=180°(∠∠∠∠等式性质).在证明五角星形五个顶角的和等于180°时,小明想通过连接CD,把五个角“凑”到△ACD内。例4已知:如图,在△ABC中,1∠是它的一个外角,E为边AC上一点,延长BC到D,连接DE.求证:1>2.∠∠证明:1∵∠是△ABC的一个外角(已知),∴∠1>3(∠三角形的一个外角大于任何一个和它不相邻的内角).∵∠3是△CDE的一个外角(外角定义).∴∠3>2(∠三角形的一个外角大于任何一个和它不相邻的内角).∴∠1>2(∠不等式的性质).CABF1345ED2例5已知:如图,P是△ABC内一点,连接PB,PC.求证:BPC∠>∠A.ABCDP证明:如图,延长BP,交AC于点D.∵∠BPC是△PDC的一个外角(外角的定义)∴∠BPC>∠PDC(三角形的一个外角大于任何一个和它不相邻的内角)∵∠PDC是△ABD的一个外角(外角的定义)∴∠PDC>∠A(三角形的一个外角大于任何一个和它不相邻的内角)∴∠BPC>∠A你还有其他的证明方法吗?ABCDP已知:如图所示.求证:(1)BDC>A;∠∠(2)BDC=A+B+C.∠∠∠∠证明(1):延长BD与AC相交于E∵∠BDC是△DCE的一个外角(外角定义),∴∠BDC>CED(∠三角形的一个外角大于和它不相邻的任何一个外角).∴∠DEC>A(∠三角形的一个外角大于和它不相邻的任何一个外角).∴∠BDC>A(∠不等式的性质).∵∠DEC是△ABE的一个外角(外角定义),BCADE已知:如图所示.求证:(1)BDC>A;∠∠(2)BDC=A+B+C.∠∠∠∠证明(2):BDC∵∠是△DCE的一个外角(外角定义),∴∠BDC=C+CED(∠∠三角形的一个外角等于和它不相邻的两个内角的和).∴∠DEC=A+B(∠∠三角形的一个外角等于和它不相邻的两个外角的和).∴∠BDC=A+B+C(∠∠∠等式的性质).∵∠DEC是△ABE的一个外角(外角定义),BCADE随堂练习1、2习题8.9数学理解