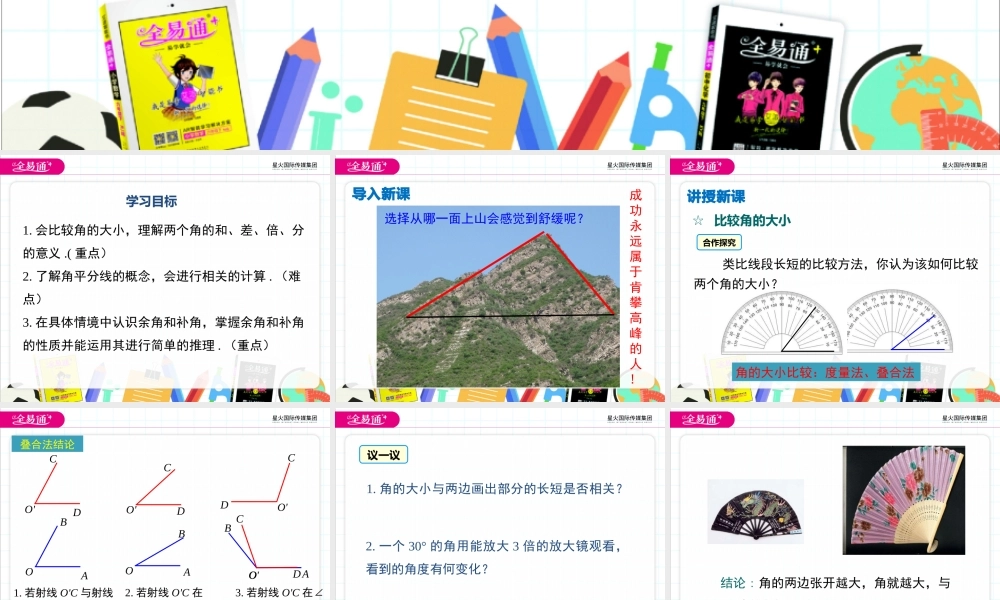
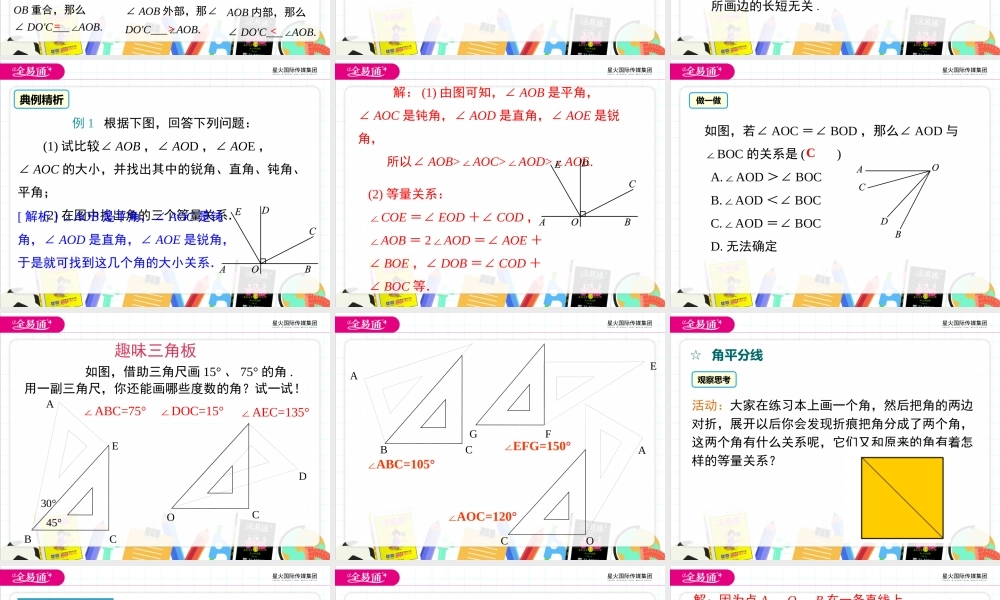
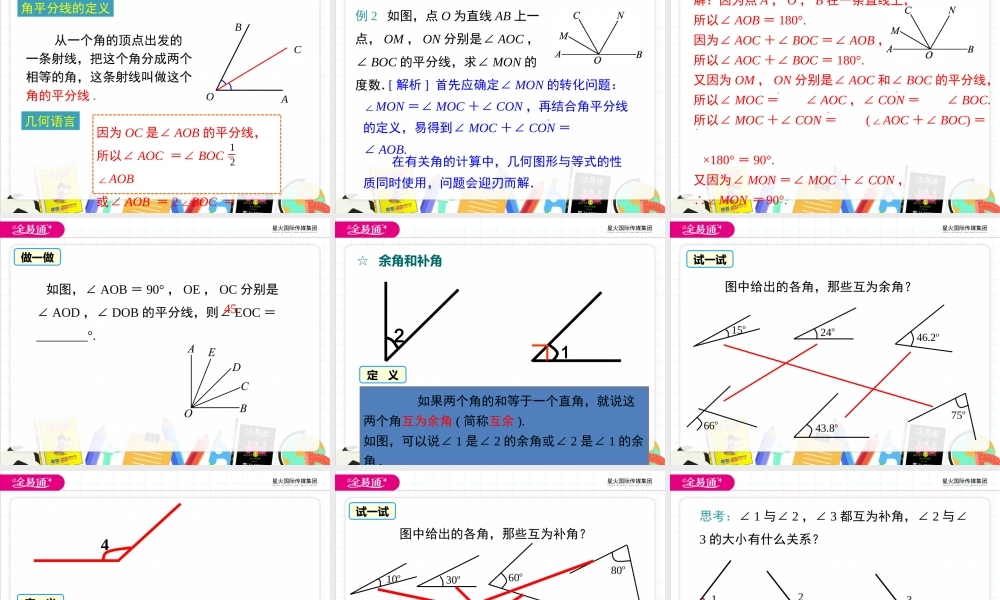
第4章直线与角4.5角的比较与补(余)角学习目标1.会比较角的大小,理解两个角的和、差、倍、分的意义.(重点)2.了解角平分线的概念,会进行相关的计算.(难点)3.在具体情境中认识余角和补角,掌握余角和补角的性质并能运用其进行简单的推理.(重点)导入新课成功永远属于肯攀高峰的人!选择从哪一面上山会感觉到舒缓呢?讲授新课☆比较角的大小合作探究类比线段长短的比较方法,你认为该如何比较两个角的大小?角的大小比较:度量法、叠合法叠合法结论OBAO'CDOBAO'CDOBAO'CD1.若射线O'C与射线OB重合,那么∠DO'C___∠AOB.2.若射线O'C在∠AOB外部,那∠DO'C___∠AOB.3.若射线O'C在∠AOB内部,那么∠DO'C___∠AOB.=>∠AOC>∠AOD>∠AOE.(2)等量关系:∠COE=∠EOD+∠COD,∠AOB=2∠AOD=∠AOE+∠BOE,∠DOB=∠COD+∠BOC等.做一做如图,若∠AOC=∠BOD,那么∠AOD与∠BOC的关系是()A.AOD∠>∠BOCB.AOD∠<∠BOCC.AOD∠=∠BOCD.无法确定C如图,借助三角尺画15°、75°的角.用一副三角尺,你还能画哪些度数的角?试一试!DOC∠ABC=75°∠DOC=15°ABC45°30°E∠AEC=135°趣味三角板ABCACO∠ABC=105°∠AOC=120°∠EFG=150°EGF☆角平分线活动:大家在练习本上画一个角,然后把角的两边对折,展开以后你会发现折痕把角分成了两个角,这两个角有什么关系呢,它们又和原来的角有着怎样的等量关系?观察思考从一个角的顶点出发的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.角平分线的定义因为OC是∠AOB的平分线,所以∠AOC=∠BOC=∠AOB或∠AOB=2∠BOC=几何语言OBAC21例2如图,点O为直线AB上一点,OM,ON分别是∠AOC,∠BOC的平分线,求∠MON的度数.[解析]首先应确定∠MON的转化问题:∠MON=∠MOC+∠CON,再结合角平分线的定义,易得到∠MOC+∠CON=∠AOB.12在有关角的计算中,几何图形与等式的性质同时使用,...