《正多边形和圆（2）》教学课件.pptVIP免费

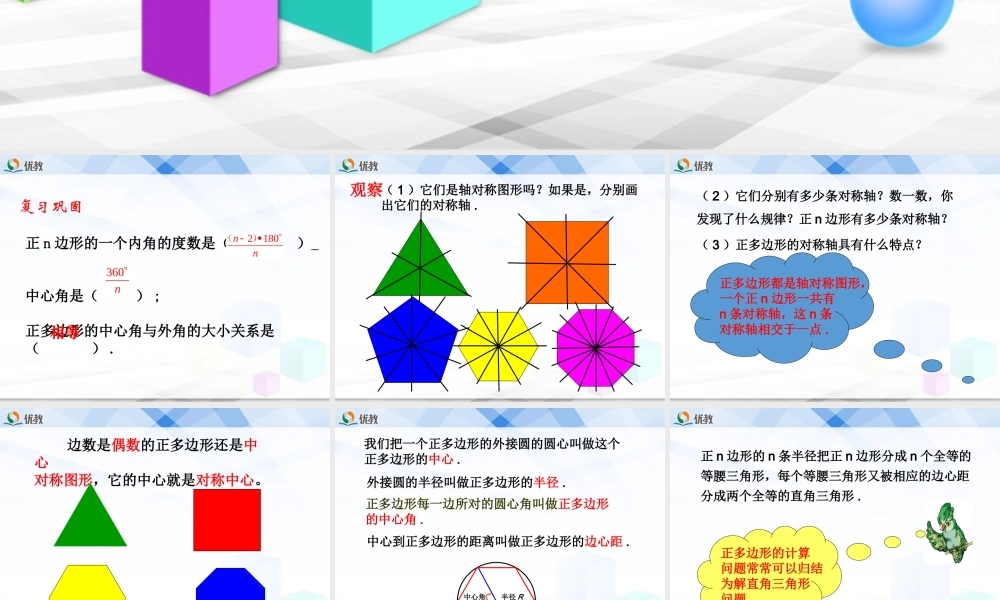
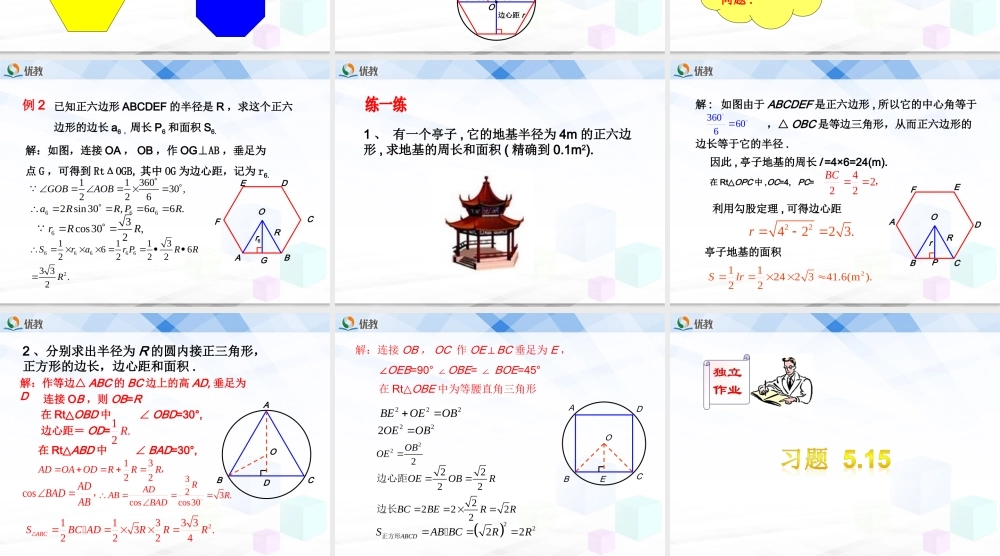
5.8正多边形和圆（二）第五章圆正n边形的一个内角的度数是（）中心角是（）;正多边形的中心角与外角的大小关系是（）.2180nn（）360n相等复习巩固观察（1）它们是轴对称图形吗？如果是，分别画出它们的对称轴.（2）它们分别有多少条对称轴？数一数，你发现了什么规律？正n边形有多少条对称轴？（3）正多边形的对称轴具有什么特点？正多边形都是轴对称图形，一个正n边形一共有n条对称轴，这n条对称轴相交于一点.边数是偶数的正多边形还是中心对称图形，它的中心就是对称中心。正多边形每一边所对的圆心角叫做正多边形的中心角.O·中心角半径R边心距r我们把一个正多边形的外接圆的圆心叫做这个正多边形的中心.外接圆的半径叫做正多边形的半径.中心到正多边形的距离叫做正多边形的边心距.正n边形的n条半径把正n边形分成n个全等的等腰三角形，每个等腰三角形又被相应的边心距分成两个全等的直角三角形.正多边形的计算问题常常可以归结为解直角三角形问题.例2已知正六边形ABCDEF的半径是R，求这个正六边形的边长a6，周长P6和面积S6.OADEFRr6CBG解：如图，连接OA，OB，作OG⊥AB，垂足为点G，可得到RtΔOGB,其中OG为边心距，记为r6.1136030,226GOBAOB6662sin30,66.aRRPaR63cos30,2rRR666662111366222233.2SrarPRRR1、有一个亭子,它的地基半径为4m的正六边形,求地基的周长和面积(精确到0.1m2).解:如图由于ABCDEF是正六边形,所以它的中心角等于，△OBC是等边三角形，从而正六边形的边长等于它的半径.360606因此,亭子地基的周长l=4×6=24(m).在Rt△OPC中,OC=4,PC=4222BC，利用勾股定理,可得边心距224223.r亭子地基的面积211242341.6(m).22SlrOABCDEFRPr2、分别求出半径为R的圆内接正三角形，正方形的边长，边心距和面积.解：作等边△ABC的BC边上的高AD,垂足为D连接OB，则OB=R在Rt△OBD中∠OBD=30°,边心距＝OD=1.2R在Rt△ABD中∠BAD=30°,1322ADOAODRRR，cosADBADAB，323.coscos30RADABRBAD2113333.2224ABCSBCADRRR·ABCDO解：连接OB，OC作OE⊥BC垂足为E，∠OEB=90°∠OBE=∠BOE=45°在Rt△OBE中为等腰直角三角形222BEOEOB222OEOB222OBOE2222OEOBR边心距22222BCBERR边长2222ABCDSABBCRR正方形·ABCDOE