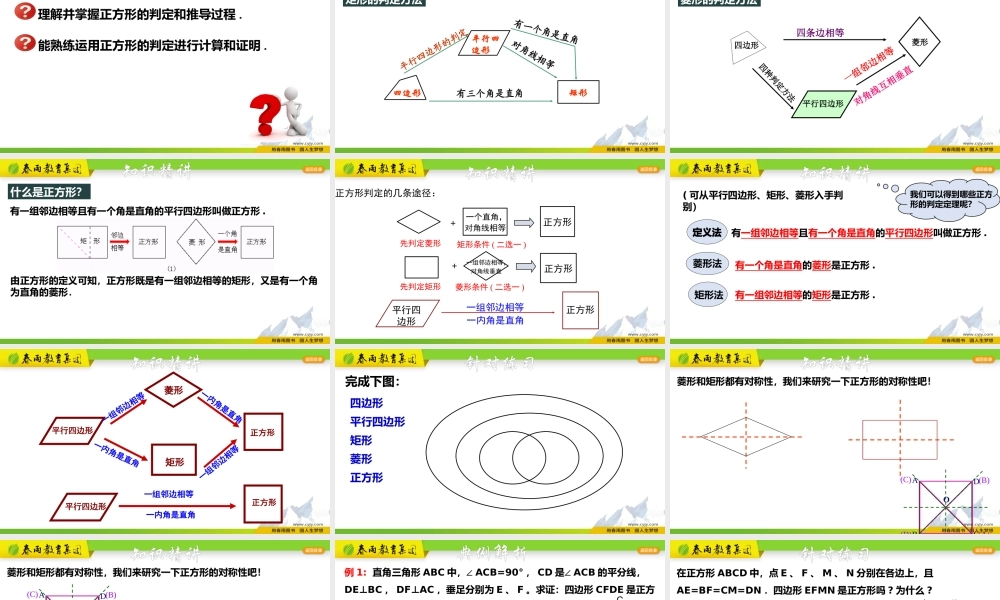
学习目标理解并掌握正方形的判定和推导过程.能熟练运用正方形的判定进行计算和证明.四边形平行四边形矩形平行四边形的判定对角线相等有一个角是直角有三个角是直角复习回顾矩形的判定方法一组邻边相等对角线互相垂直四条边相等四种判定方法四边形平行四边形菱形菱形的判定方法复习回顾由正方形的定义可知,正方形既是有一组邻边相等的矩形,又是有一个角为直角的菱形.有一组邻边相等且有一个角是直角的平行四边形叫做正方形.什么是正方形?知识精讲正方形判定的几条途径:正方形正方形++先判定菱形先判定矩形矩形条件(二选一)菱形条件(二选一)一个直角,一组邻边相等,对角线相等对角线垂直平行四边形正方形一组邻边相等一内角是直角知识精讲(可从平行四边形、矩形、菱形入手判别)有一组邻边相等且有一个角是直角的平行四边形叫做正方形.定义法菱形法矩形法有一个角是直角的菱形是正方形.有一组邻边相等的矩形是正方形.我们可以得到哪些正方形的判定定理呢?知识精讲平行四边形正方形矩形菱形一组邻边相等一组邻边相等一内角是直角一内角是直角平行四边形正方形一组邻边相等一内角是直角知识精讲四边形平行四边形矩形菱形正方形完成下图:针对练习OABCD(A)(B)(C)(D)菱形和矩形都有对称性,我们来研究一下正方形的对称性吧!知识精讲OABCD(A)(B)(C)(D)菱形和矩形都有对称性,我们来研究一下正方形的对称性吧!知识精讲且正方形有4条对称轴由此可见,正方形既是轴对称图形也是中心对称图形.例1:直角三角形ABC中,∠ACB=90°,CD是∠ACB的平分线,DE⊥BC,DF⊥AC,垂足分别为E、F。求证:四边形CFDE是正方形.FEDCBA21典例解析证明: DE⊥AC,DF⊥AB,∴∠DEC=90°,∠DFC=90°,而∠ACB=90°∴四边形ABCD为矩形. CD平分∠ACB,DE⊥AC,DF⊥BC∴DE=DF.∴四边形ABCD是正方形.在正方形ABCD中,点E、F、M、N分别在各边上,且AE=BF=CM=DN.四边形EFMN是正方形吗?为什么?证明: 四边形ABCD是正方形,∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°. AE=BF=CM=DN,∴AN=BE=CF=DM.分析:由已知可证△AEN≌△BFE≌△CMF≌△DNM,得四边形EFMN是菱形,再证有一个角是直角即可.针对练习在△AEN、△BFE、△CMF、△DNM中,AE=BF=CM=DN,∠A=∠B=∠C=∠D,AN=BE=CF=DM,∴△AEN≌△BFE≌△CMF≌△DNM,∴EN=FE=MF=NM,∠ANE=∠BEF,∴四边形EFMN是菱形,∠NEF=180°-(∠AEN+∠BEF)=180°-(∠AEN+∠ANE)=180°-90°=90°.∴四边形EFMN是正方形.针对练习例2:如图,四边...