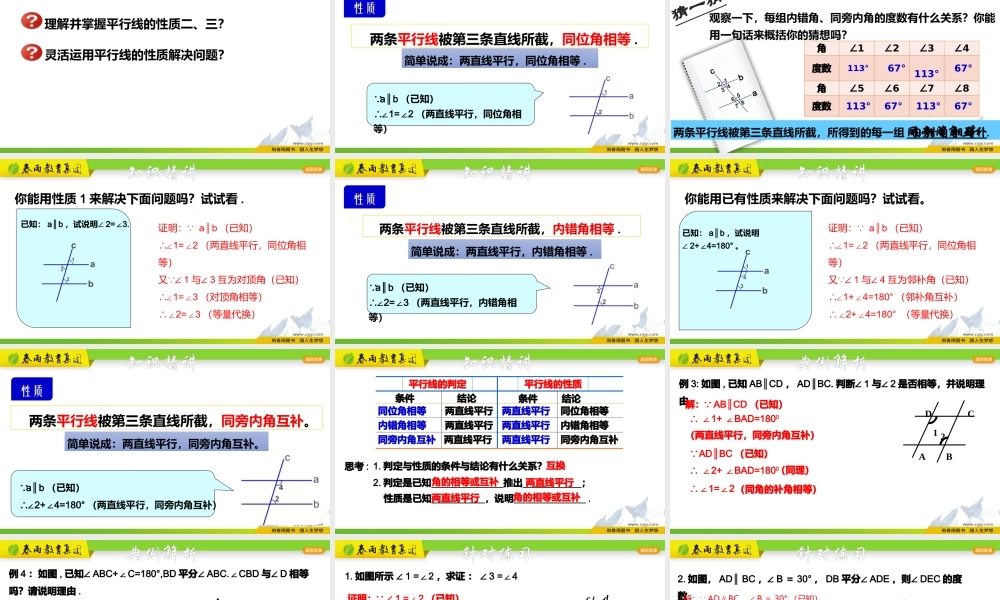
理解并掌握平行线的性质二、三?灵活运用平行线的性质解决问题?学习任务复习回顾性质1两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等. a∥b(已知)∴∠1=2∠(两直线平行,同位角相等)复习回顾abc21345678观察一下,每组内错角、同旁内角的度数有什么关系?你能用一句话来概括你的猜想吗?猜一猜角∠1∠2∠3∠4度数113°67°113°67°角∠5∠6∠7∠8度数113°67°113°67°两条平行线被第三条直线所截,所得到的每一组_____________.内错角相等同旁内角互补已知:a∥b,试说明∠2=3.∠知识精讲你能用性质1来解决下面问题吗?试试看.证明: a∥b(已知)∴∠1=2∠(两直线平行,同位角相等)又 ∠1与∠3互为对顶角(已知)∴∠1=3∠(对顶角相等)∴∠2=3∠(等量代换)知识精讲性质2两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等. a∥b(已知)∴∠2=3∠(两直线平行,内错角相等)知识精讲你能用已有性质来解决下面问题吗?试试看。证明: a∥b(已知)∴∠1=2∠(两直线平行,同位角相等)又 ∠1与∠4互为邻补角(已知)∴∠1+4=180°∠(邻补角互补)∴∠2+4=180°∠(等量代换)已知:a∥b,试说明∠2+4=180°∠。知识精讲性质3两条平行线被第三条直线所截,同旁内角互补。简单说成:两直线平行,同旁内角互补。 a∥b(已知)∴∠2+4=180°∠(两直线平行,同旁内角互补)同位角相等两直线平行两直线平行同位角相等平行线的判定平行线的性质条件结论条件结论思考:1.判定与性质的条件与结论有什么关系?互换内错角相等两直线平行两直线平行内错角相等同旁内角互补两直线平行两直线平行同旁内角互补2.判定是已知推出;角的相等或互补两直线平行性质是已知,说明.两直线平行角的相等或互补知识精讲例3:如图,已知ABCD∥,ADBC.∥判断∠1与∠2是否相等,并说明理由.ABCD12解: ABCD∥(已知)∴∠1+BAD=180∠0(两直线平行,同旁内角互补)∴∠1=2∠(同角的补角相等) ADBC∥(已知)∴∠2+BAD=180∠0(同理)典例解析例4:如图,已知∠ABC+C=180°,BD∠平分∠ABC.CBD∠与∠D相等吗?请说明理由.ABDC解:∠CBD=D∠。理由如下: ∠ABC+C=180∠0(已知)∴ABCD∥(同旁内角互补,两直线平行)∴∠D=ABD∠(两直线平行,内错角相等)又 BD平分∠ABC∴∠CBD=ABD=D∠∠典例解析cdab34211.如图所示∠1=2∠,求证:∠3=4∠证明: ∠1=2∠(已知)∴a//b(同位角相等,两直线平行)∴∠...