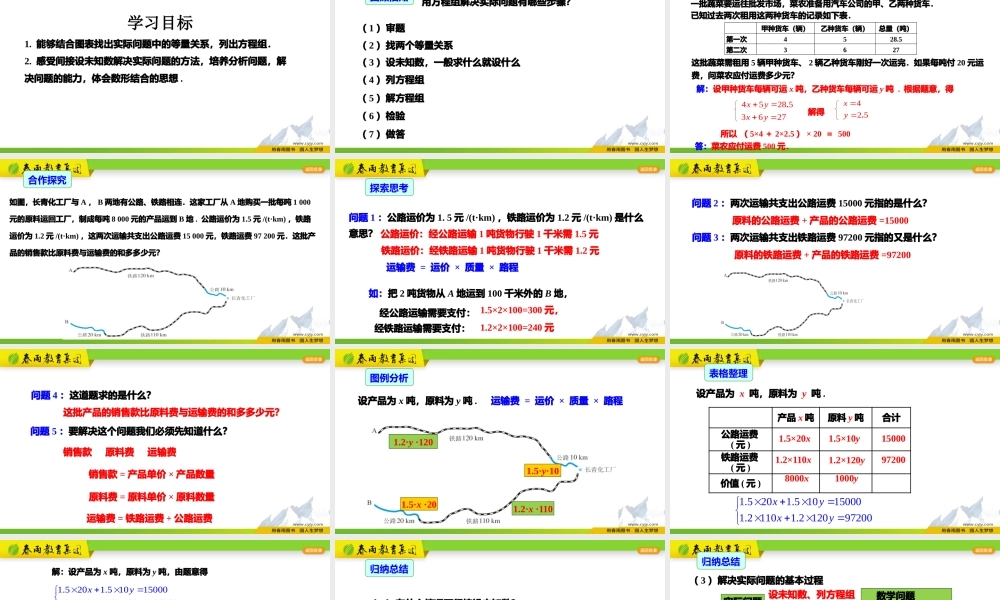
8.3实际问题与二元一次方程组第3课时人教版七年级下学习目标1.能够结合图表找出实际问题中的等量关系,列出方程组.2.感受间接设未知数解决实际问题的方法,培养分析问题,解决问题的能力,体会数形结合的思想.用方程组解决实际问题有哪些步骤?(3)设未知数,一般求什么就设什么(2)找两个等量关系(4)列方程组(5)解方程组(6)检验回顾旧知(1)审题(7)做答一批蔬菜要运往批发市场,菜农准备用汽车公司的甲、乙两种货车.已知过去两次租用这两种货车的记录如下表.甲种货车(辆)乙种货车(辆)总量(吨)第一次4528.5第二次3627这批蔬菜需租用5辆甲种货车、2辆乙种货车刚好一次运完.如果每吨付20元运费,问菜农应付运费多少元?解:设甲种货车每辆可运x吨,乙种货车每辆可运y吨.根据题意,得452853627xyxy.解得425xy.所以(5×4+2×2.5)×20=500答:菜农应付运费500元.引入新课如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费97200元.这批产品的销售款比原料费与运输费的和多多少元?合作探究问题1:公路运价为1.5元/(t·km),铁路运价为1.2元/(t·km)是什么意思?如:把2吨货物从A地运到100千米外的B地,经公路运输需要支付:公路运价:经公路运输1吨货物行驶1千米需1.5元铁路运价:经铁路运输1吨货物行驶1千米需1.2元1.5×2×100=300元,1.2×2×100=240元运输费=运价×质量×路程经铁路运输需要支付:探索思考问题2:两次运输共支出公路运费15000元指的是什么?原料的公路运费+产品的公路运费=15000问题3:两次运输共支出铁路运费97200元指的又是什么?原料的铁路运费+产品的铁路运费=97200问题4:这道题求的是什么?这批产品的销售款比原料费与运输费的和多多少元?问题5:要解决这个问题我们必须先知道什么?销售款原料费运输费销售款=产品单价×产品数量原料费=原料单价×原料数量运输费=铁路运费+公路运费设产品为x吨,原料为y吨.1.2·y·1201.5·y·101.5·x·201.2·x·110运输费=运价×质量×路程图例分析产品x吨原料y吨合计公路运费(元)铁路运费(元)价值(元)1.5×20x1.5×10y150001.2×110x1.2×120y972008000x1000y设产品为x吨,原料为y吨.1.5201.510150001.21101.212097200xyxy表格整理解:设产品为x吨...