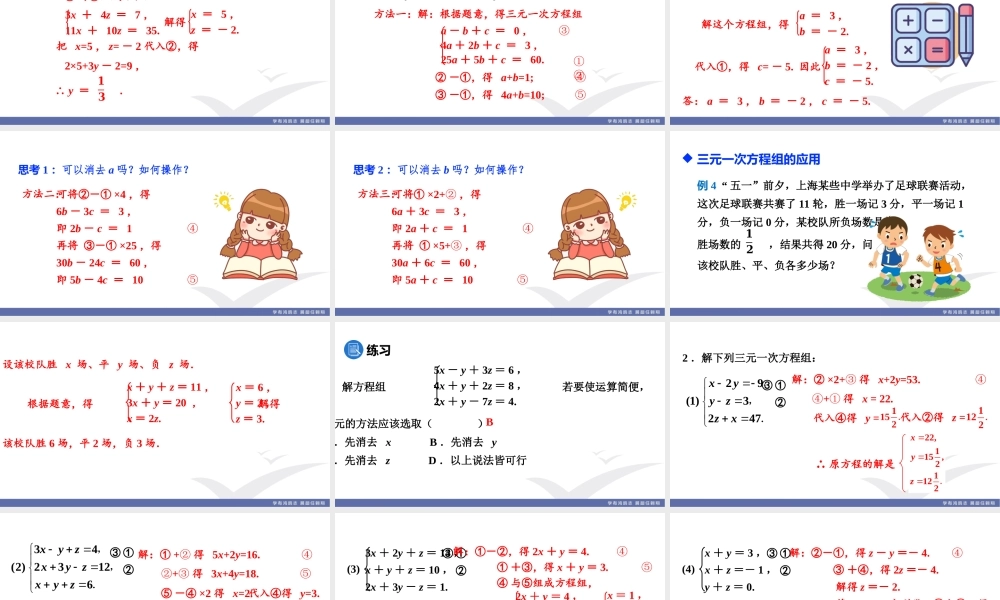
第八章二元一次方程组8.4三元一次方程组的解法导入新课1.解二元一次方程组有哪几种方法?2.解二元一次方程组的基本思路是什么?将二元一次方程组通过“代入”或“加减”进行消元成一元一次方程.代入消元法和加减消元法.回顾二元一次方程组的解法消元法化归转化思想探究新知小明手头有12张面额分别为1元、2元、5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的4倍.求1元、2元、5元纸币各多少张?思考:(1)该题中有几个等量关系?分别是什么?(2)如果设1元、2元、5元的纸币分别为x张、y张、z张,那么可列出怎样的方程组?三元一次方程组的概念探究设1元、2元和5元的纸币分别为x张、y张和z张.则可列出方程组:你能说说什么叫三元一次方程组吗?x+y+z=12,x+2y+5z=22,x=4y.含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组.知识归纳思考x+y+z=12,x+2y+5z=22,x=4y.怎么解呢?方程组能不能类比二元一次方程组的解法来求解?思路:x+y+z=12,x+2y+5z=22,x=4y.①②③将③代入①②,得4y+y+z=12,4y+2y+5z=22.即5y+z=12,6y+5z=22.再求解出二元一次方程组,将y的值代入③中可得z的值.解三元一次方程组的基本思路知识归纳消元法:通过“代入”或“加减”进行消元,把“三元”转化为“二元”,使解三元一次方程组转化为解二元一次方程组,进而再转化为解一元一次方程.三元一次方程组二元一次方程组一元一次方程消元消元例题与练习例1下列方程组中,是三元一次方程组的是()2x+y=7,5x-2y=3,2x-y=5x-y=2,y-z=3,z-m=4a=2,b=3,b-c=4xy+z=2,x+yz=4,xz+y=6A.B.C.D.C思考:对于这个方程组,消哪个元比较方便?为什么?3472395978xzxyzxyz,,.例2解三元一次方程组:①②③思路:方程①只含x、z,因此,可以由②③消去y,得到的方程可与①组成一个二元一次方程组.解:②×3+③,得11x+10z=35.④①与④组成方程组把x=5,z=-2代入②,得2×5+3y-2=9,3x+4z=7,11x+10z=35.解得x=5,z=-2.∴y=.𝟏𝟑例3在等式y=ax2+bx+c中,当x=-1时,y=0;当x=2时,y=3;当x=5时,y=60,求a,b,c的值.方法一:解:根据题意,得三元一次方程组②-①,得a+b=1;④③-①,得4a+b=10;⑤①②③a-b+c=0,4a+2b+c=3,25a+5b+c=60.答:a=3,b=-2,c=-5.④与⑤组成方程组a+b=1,4a+b=10.解...