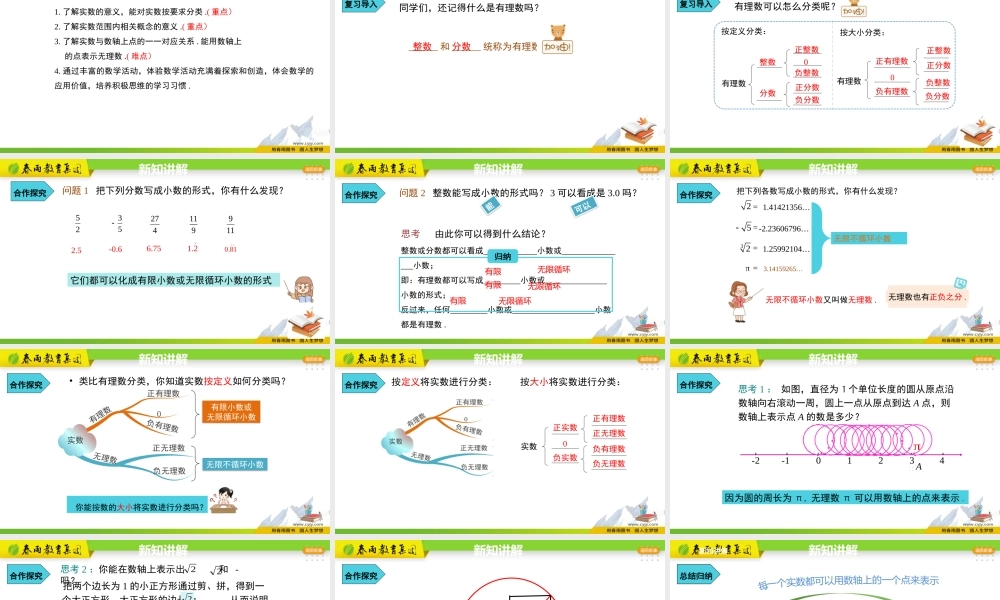
第六章实数6.3实数第1课时人教版同步课件学习目标1.了解实数的意义,能对实数按要求分类.(重点)2.了解实数范围内相关概念的意义.(重点)3.了解实数与数轴上点的一一对应关系.能用数轴上的点表示无理数.(难点)4.通过丰富的数学活动,体验数学活动充满着探索和创造,体会数学的应用价值,培养积极思维的学习习惯.复习导入同学们,还记得什么是有理数吗?______和______统称为有理数.分数整数新知导入整数正整数分数正整数负整数0正分数负分数正有理数负有理数正分数负整数负分数按定义分类:按大小分类:有理数0有理数复习导入有理数可以怎么分类呢?新知导入问题1把下列分数写成小数的形式,你有什么发现?25534271191192.5-0.66.751.20.81合作探究它们都可以化成有限小数或无限循环小数的形式新知讲解整数或分数都可以看成小数或小数;即:有理数都可以写成小数或小数的形式;反过来,任何小数或小数都是有理数.归纳问题2整数能写成小数的形式吗?3可以看成是3.0吗?有限无限循环有限无限循环有限无限循环合作探究能可以思考由此你可以得到什么结论?新知讲解3.14159265…32=5=2=π=把下列各数写成小数的形式,你有什么发现?-2.23606796…1.25992104…1.41421356…无限不循环小数无限不循环小数又叫做无理数.无理数也有正负之分.合作探究新知讲解•类比有理数分类,你知道实数按定义如何分类吗?有理数实数无理数正有理数0负有理数正无理数负无理数有限小数或无限循环小数无限不循环小数你能按数的大小将实数进行分类吗?合作探究新知讲解按大小将实数进行分类:正有理数正实数负实数正无理数0实数负有理数负无理数按定义将实数进行分类:合作探究新知讲解思考1:如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达A点,则数轴上表示点A的数是多少?因为圆的周长为π,无理数π可以用数轴上的点来表示.合作探究0-2-11324π●●●●●●●●●●●●●●A新知讲解222思考2:你能在数轴上表示出和-吗?221111把两个边长为1的小正方形通过剪、拼,得到一个大正方形,大正方形的边长为,从而说明边长为1的小正方形的对角线为.22合作探究新知讲解-2-1012222-每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一点都表示一个实数.合作探究新知讲解实数数轴上的点一一对应总结归纳新知讲解总结归纳新知讲解把下列各数填入相应的大括号内:有理数:{}无理数:{}31291193823234.2013.1010010001......