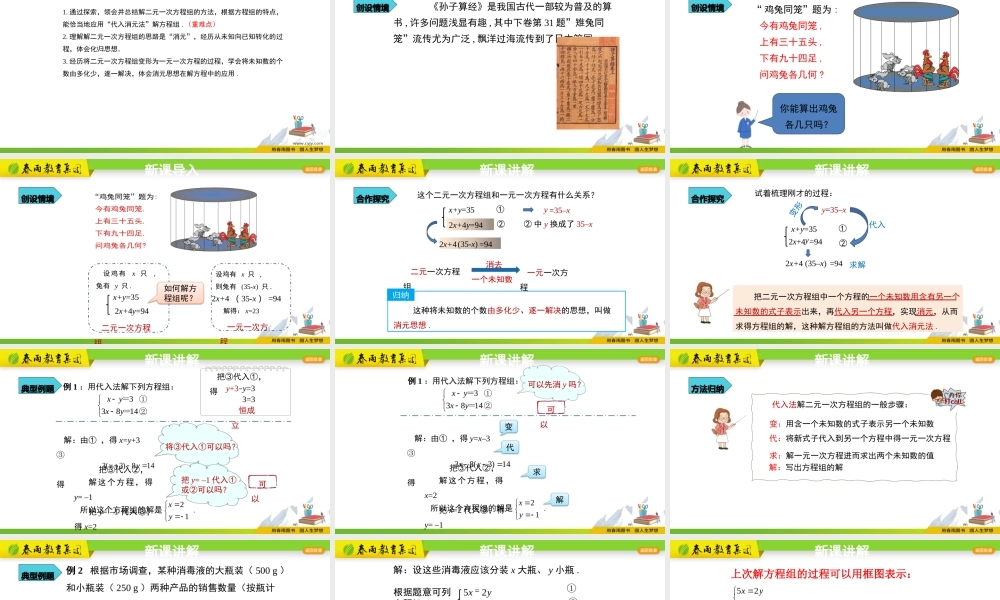
人教版同步课件8.2消元-二元一次方程组第1课时人教版八年级下1.通过探索,领会并总结解二元一次方程组的方法,根据方程组的特点,能恰当地应用“代入消元法”解方程组.(重难点)2.理解解二元一次方程组的思路是“消元”,经历从未知向已知转化的过程,体会化归思想.3.经历将二元一次方程组变形为一元一次方程的过程,学会将未知数的个数由多化少,逐一解决,体会消元思想在解方程中的应用.学习目标创设情境《孙子算经》是我国古代一部较为普及的算书,许多问题浅显有趣,其中下卷第31题”雉兔同笼”流传尤为广泛,飘洋过海流传到了日本等国.新课导入创设情境“鸡兔同笼”题为:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?你能算出鸡兔各几只吗?新课导入设鸡有x只,兔有y只.x+y=352x+4y=94二元一次方程组设鸡有x只,则兔有(35-x)只.2x+4(35-x)=94一元一次方程解得:x=23如何解方程组呢?创设情境新课导入x+y=352x+4y=942x+4=94(35-x)一元一次方程这个二元一次方程组和一元一次方程有什么关系?①②②中y换成了35–x二元一次方程组消去一个未知数y归纳这种将未知数的个数由多化少、逐一解决的思想,叫做消元思想.=35–x合作探究新课讲解x+y=352x+4=94y2x+4=94(35–x)试着梳理刚才的过程:①②y=35–x把二元一次方程组中一个方程的一个未知数用含有另一个未知数的式子表示出来,再代入另一个方程,实现消元,从而求得方程组的解,这种解方程组的方法叫做代入消元法.变形代入求解合作探究新课讲解例1:用代入法解下列方程组:解:由①,得x=y+3③把③代入②,得3(3)814yy解这个方程,得y=–1把y=–1代入③,得x=2所以这个方程组的解是.21xy将③代入①可以吗?把③代入①,得y+3–y=33=3恒成立把y=–1代入①或②可以吗?可以33814xyxy=①=②典型例题新课讲解例1:用代入法解下列方程组:可以先消y吗?可以解:由①,得y=x–3③把③代入②,得解这个方程,得x=2把x=2代入③,得y=–1所以这个方程组的解是.21xy38(3)14xx变代求解33814xyxy=①=②新课讲解代入法解二元一次方程组的一般步骤:代:将新式子代入到另一个方程中得一元一次方程解:写出方程组的解方法归纳变:用含一个未知数的式子表示另一个未知数求:解一元一次方程进而求出两个未知数的值新课讲解例2根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g)两种产品的销售数量(按瓶计算)比为2:5.某厂每天生产...