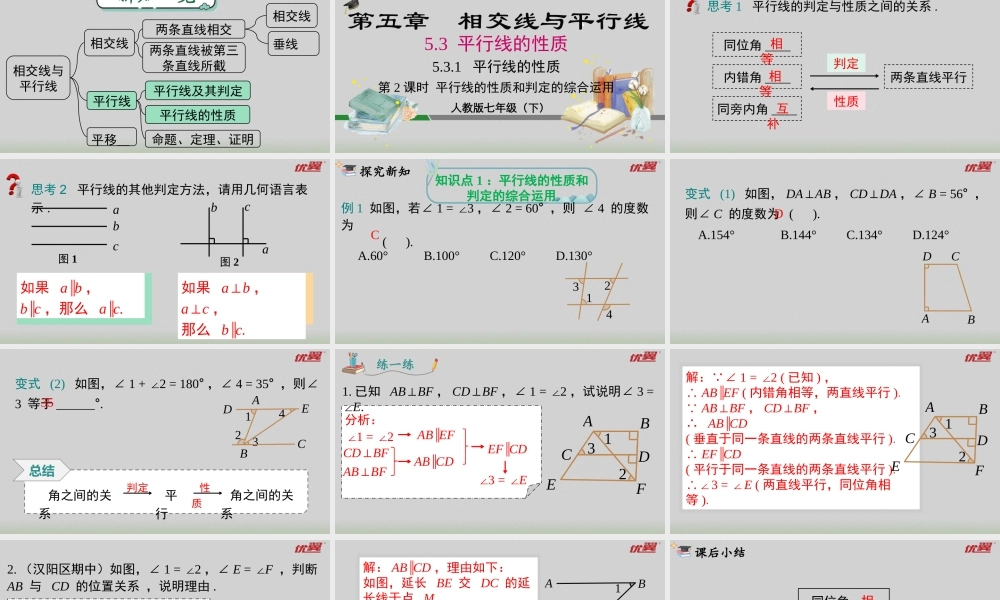
优质教学资源合集优翼与一线教师联合编写,为各位老师提供优质的原创资源,内含教学课件、教案、配套习题课件、原创模拟卷、课文朗读音视频等资料。实时更新!扫码关注!原创新知一览相交线平行线平行线及其判定平移相交线与平行线平行线的性质两条直线相交两条直线被第三条直线所截相交线垂线新知一览命题、定理、证明人教版七年级(下)第五章相交线与平行线5.3平行线的性质5.3.1平行线的性质第2课时平行线的性质和判定的综合运用导入新课思考1平行线的判定与性质之间的关系.内错角____同位角____两条直线平行同旁内角____相等相等互补判定性质思考2平行线的其他判定方法,请用几何语言表示.abc图1abc图2如果a∥b,b∥c,那么a∥c.如果a⊥b,a⊥c,那么b∥c.探究新知知识点1:平行线的性质和判定的综合运用例1如图,若∠1=3∠,∠2=60°,则∠4的度数为().A.60°B.100°C.120°D.130°4321C变式(1)如图,DA⊥AB,CD⊥DA,∠B=56°,则∠C的度数为().A.154°B.144°C.134°D.124°BADCD变式(2)如图,∠1+2=180∠°,∠4=35°,则∠3等于______°.354321CDEAB总结角之间的关系平行角之间的关系性质判定练一练分析:∠1=2∠AB∥EF1.已知AB⊥BF,CD⊥BF,∠1=2∠,试说明∠3=∠E.CD⊥BFAB∥CDAB⊥BFEF∥CD∠3=∠E321CDEFAB解: ∠1=2∠(已知),∴AB∥EF(内错角相等,两直线平行). AB⊥BF,CD⊥BF,∴AB∥CD(垂直于同一条直线的两条直线平行).∴EF∥CD(平行于同一条直线的两条直线平行).3=∴∠∠E(两直线平行,同位角相等).321CDEFAB2.(汉阳区期中)如图,∠1=2∠,∠E=∠F,判断AB与CD的位置关系,说明理由.21ABEFDCM分析:判断AB∥CD与两条直线相截的第三条直线延长BE交DC的延长线于M先证BM∥FC∠M=1∠∠M=2∠21ABEFDCM解:AB∥CD,理由如下:如图,延长BE交DC的延长线于点M, ∠BEF=∠F,∴BM∥FC.∴∠M=2∠.1=2 ∠∠,∴∠M=1∠.∴AB∥CD.课后小结同位角______内错角______同旁内角_____相等相等互补两直线平行判定性质求角的度数,说明角相等或互补应用当堂练习1.如图,在四边形ABCD,连接BD,延长AB至点E.添加一个条件,使AD∥BC,请写出三种不同的条件.条件一:_______________;条件二:_______________;条件三:_______________.∠2=5∠∠A=3∠∠A+∠CBA=180°31245AEDBC2.如图,C、D是直线AB上的两点,∠1+2=∠180°,DE平分∠CDF,EF∥AB.(1)CE与DF平行吗?为什么?(2)若∠DCE=130°,求∠DEF的度数.EF∥AB∠1+2=180∠°∠2=∠DCE(1)...