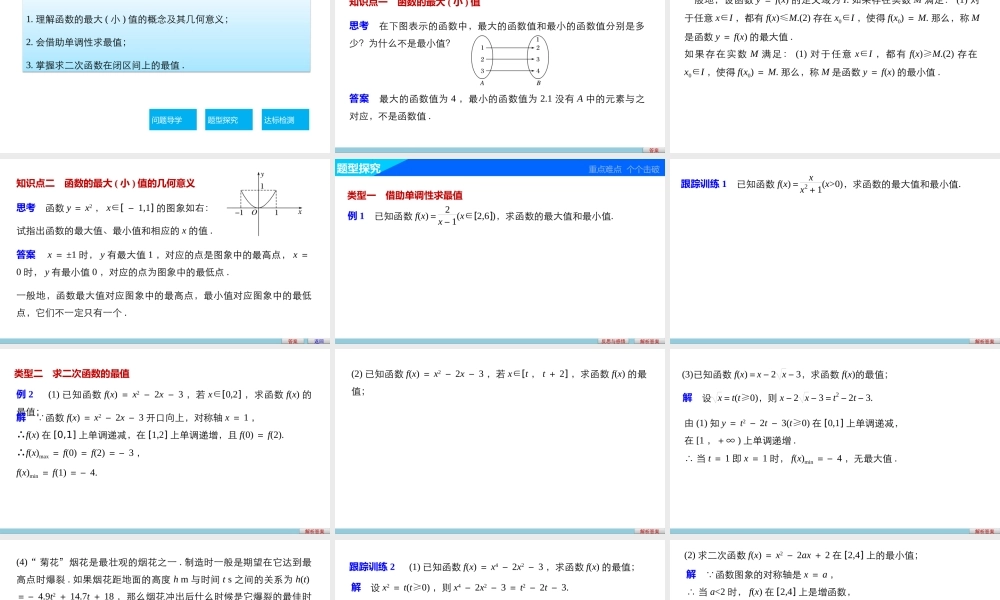
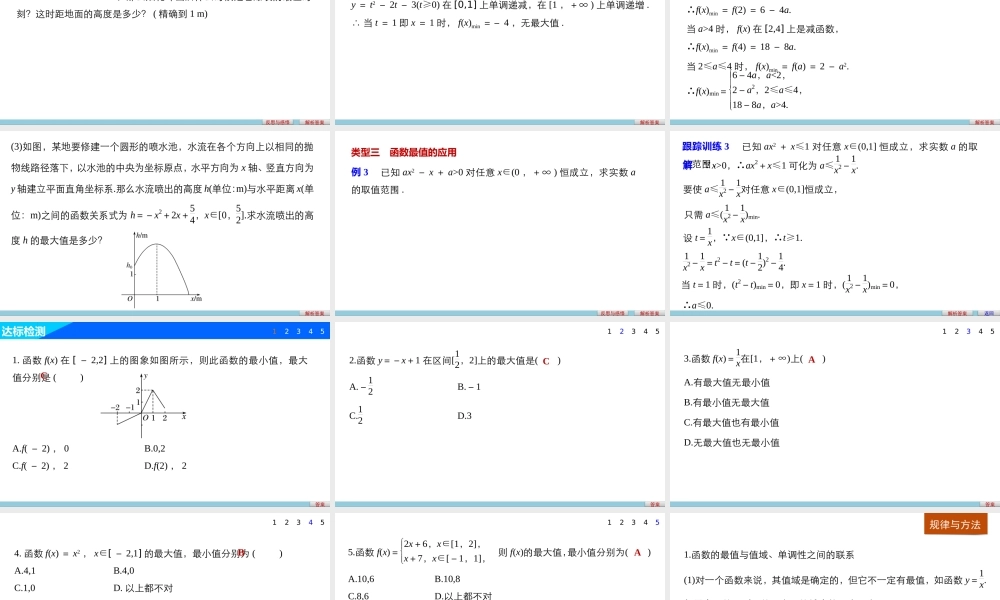
第2课时函数的最大(小)值第一章1.3.1单调性与最大(小)值1.理解函数的最大(小)值的概念及其几何意义;2.会借助单调性求最值;3.掌握求二次函数在闭区间上的最值.问题导学题型探究达标检测学习目标问题导学新知探究点点落实知识点一函数的最大(小)值思考在下图表示的函数中,最大的函数值和最小的函数值分别是多少?为什么不是最小值?答案答案最大的函数值为4,最小的函数值为2.1没有A中的元素与之对应,不是函数值.一般地,设函数y=f(x)的定义域为I.如果存在实数M满足:(1)对于任意x∈I,都有f(x)≤M.(2)存在x0∈I,使得f(x0)=M.那么,称M是函数y=f(x)的最大值.如果存在实数M满足:(1)对于任意x∈I,都有f(x)≥M.(2)存在x0∈I,使得f(x0)=M.那么,称M是函数y=f(x)的最小值.知识点二函数的最大(小)值的几何意义思考函数y=x2,x∈[-1,1]的图象如右:答案试指出函数的最大值、最小值和相应的x的值.答案x=±1时,y有最大值1,对应的点是图象中的最高点,x=0时,y有最小值0,对应的点为图象中的最低点.一般地,函数最大值对应图象中的最高点,最小值对应图象中的最低点,它们不一定只有一个.返回题型探究重点难点个个击破类型一借助单调性求最值例1已知函数f(x)=2x-1(x∈[2,6]),求函数的最大值和最小值.解析答案反思与感悟解析答案跟踪训练1已知函数f(x)=xx2+1(x>0),求函数的最大值和最小值.类型二求二次函数的最值例2(1)已知函数f(x)=x2-2x-3,若x∈[0,2],求函数f(x)的最值;解析答案解 函数f(x)=x2-2x-3开口向上,对称轴x=1,∴f(x)在[0,1]上单调递减,在[1,2]上单调递增,且f(0)=f(2).∴f(x)max=f(0)=f(2)=-3,f(x)min=f(1)=-4.解析答案(2)已知函数f(x)=x2-2x-3,若x∈[t,t+2],求函数f(x)的最值;解析答案由(1)知y=t2-2t-3(t≥0)在[0,1]上单调递减,在[1,+∞)上单调递增.∴当t=1即x=1时,f(x)min=-4,无最大值.(3)已知函数f(x)=x-2x-3,求函数f(x)的最值;解设x=t(t≥0),则x-2x-3=t2-2t-3.解析答案(4)“菊花”烟花是最壮观的烟花之一.制造时一般是期望在它达到最高点时爆裂.如果烟花距地面的高度hm与时间ts之间的关系为h(t)=-4.9t2+14.7t+18,那么烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少?(精确到1m)反思与感悟解析答案跟踪训练2(1)已知函数f(x)=x4-2x2-3,求函数f(x)的最值;解设x2=t(t≥0),则x4-2x2-3=t2-2t-3.y=t2-2t-3(t≥0)在[0,1]上单调递...