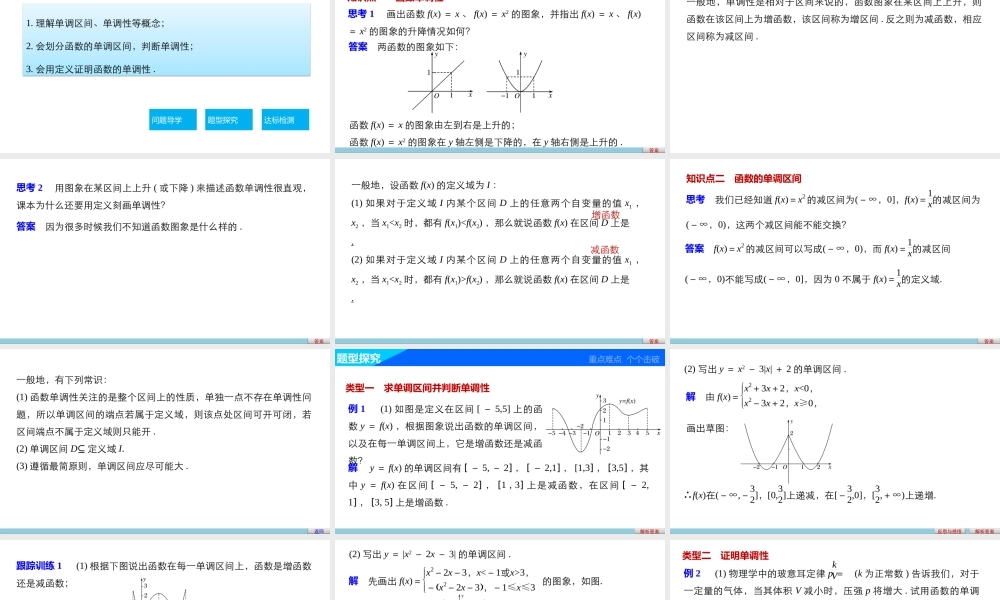
第1课时函数的单调性第一章1.3.1单调性与最大(小)值1.理解单调区间、单调性等概念;2.会划分函数的单调区间,判断单调性;3.会用定义证明函数的单调性.问题导学题型探究达标检测学习目标问题导学新知探究点点落实知识点一函数单调性思考1画出函数f(x)=x、f(x)=x2的图象,并指出f(x)=x、f(x)=x2的图象的升降情况如何?答案答案两函数的图象如下:函数f(x)=x的图象由左到右是上升的;函数f(x)=x2的图象在y轴左侧是下降的,在y轴右侧是上升的.一般地,单调性是相对于区间来说的,函数图象在某区间上上升,则函数在该区间上为增函数,该区间称为增区间.反之则为减函数,相应区间称为减区间.思考2用图象在某区间上上升(或下降)来描述函数单调性很直观,课本为什么还要用定义刻画单调性?答案答案因为很多时候我们不知道函数图象是什么样的.一般地,设函数f(x)的定义域为I:(1)如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1f(x2),那么就说函数f(x)在区间D上是.答案增函数减函数知识点二函数的单调区间思考我们已经知道f(x)=x2的减区间为(-∞,0],f(x)=1x的减区间为(-∞,0),这两个减区间能不能交换?答案答案f(x)=x2的减区间可以写成(-∞,0),而f(x)=1x的减区间(-∞,0)不能写成(-∞,0],因为0不属于f(x)=1x的定义域.一般地,有下列常识:(1)函数单调性关注的是整个区间上的性质,单独一点不存在单调性问题,所以单调区间的端点若属于定义域,则该点处区间可开可闭,若区间端点不属于定义域则只能开.(2)单调区间D⊆定义域I.(3)遵循最简原则,单调区间应尽可能大.返回题型探究重点难点个个击破类型一求单调区间并判断单调性例1(1)如图是定义在区间[-5,5]上的函数y=f(x),根据图象说出函数的单调区间,以及在每一单调区间上,它是增函数还是减函数?解析答案解y=f(x)的单调区间有[-5,-2],[-2,1],[1,3],[3,5],其中y=f(x)在区间[-5,-2],[1,3]上是减函数,在区间[-2,1],[3,5]上是增函数.解析答案(2)写出y=x2-3|x|+2的单调区间.解由f(x)=x2+3x+2,x<0,x2-3x+2,x≥0,画出草图:∴f(x)在(-∞,-32],[0,32]上递减,在[-32,0],[32,+∞)上递增.反思与感悟解析答案跟踪训练1(1)根据下图说出函数在每一单调区间上,函数是增函数还是减函数;...