高中数学人教A版选修1-1课件：3.2.1《几个常用函数的导数》.pptVIP免费

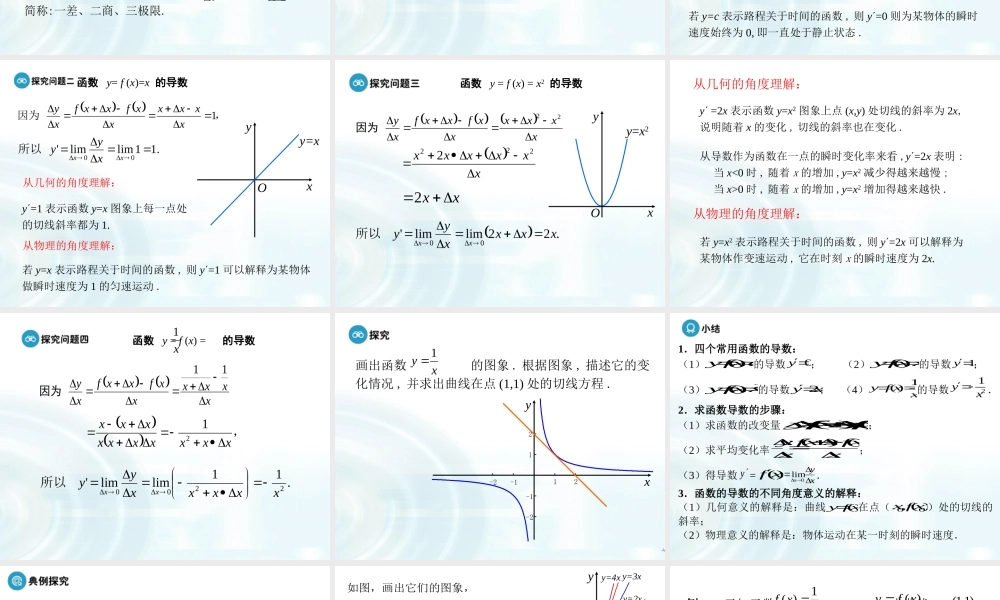
第3章导数及应用3.2.1几个常用函数的导数几个常用函数的导数内容：根据导数的定义求四个常用函数的导数应用根据导数定义求出函数的导数求曲线在某点处的切线方程本课主要学习根据导数定义求出几个常用函数的导数,利用地球脉动视频引入新课,以“问题引导，探究交流”为主，新知识是学生在已有知识的基础上探究而来，例题的处理非常灵活，变式训练设计合理，过渡有水到渠成之感，整堂课下来充实流畅.在讲述利用导数求切线方程时，采用例题与思考与探究相结合的方法，通过2个例题。随后是课堂检测，通过设置难易不同的必做和选做试题，有利于对不同的学生进行因材施教。一般地，函数y=f(x)在x=x0处的瞬间变化率是0000()()limlimxxfxxfxyxx，我们称它为()fx在点0xx处的导数，记为()fx，或0|xxy，即：0000()()()limlimxxfxxfxyfxxx.1.导数的定义是什么？曲线)(xfy在点（)(,00xfx）处的切线的斜率．3.求函数)(xfy的导数的一般步骤是什么？（1）求函数的改变量y()()fxxfx；（2）求平均变化率yx()()fxxfxx；（3）取极限，得导数y=()fxxyx0lim=0()()limxfxxfxx．简称:一差、二商、三极限.2.导数的几何意义是什么？地球的变幻—导数与函数的变幻地球脉动函数y=f(x)=c的导数y=cyxO，因0xccxxfxxfxy00'limlim0.0xxyyx所以y=0表示函数y=x图象上每一点处的切线的斜率都为0.若y=c表示路程关于时间的函数,则y=0则为某物体的瞬时速度始终为0,即一直处于静止状态.从几何的角度理解：从物理的角度理解：函数y=f(x)=x的导数，因为1xxxxxxfxxfxy.11limlim'00xxxyy所以y=xyxOy=1表示函数y=x图象上每一点处的切线斜率都为1.若y=x表示路程关于时间的函数,则y=1可以解释为某物体做瞬时速度为1的匀速运动.从几何的角度理解：从物理的角度理解：函数y=f(x)=x2的导数xxxxxxfxxfxy22因为xxxxxx2222xx2.22limlim'00xxxxyyxx所以y=x2yxOy=2x表示函数y=x2图象上点(x,y)处切线的斜率为2x,说明随着x的变化,切线的斜率也在变化.从导数作为函数在一点的瞬时变化率来看,y=2x表明:当x<0时,随着x的增加,y=x2减少得越来越慢;当x>0时,随着x的增加,y=x2增加得...