高中数学人教A版必修5《2.6等比数列的前n项和2》课件.pptVIP免费

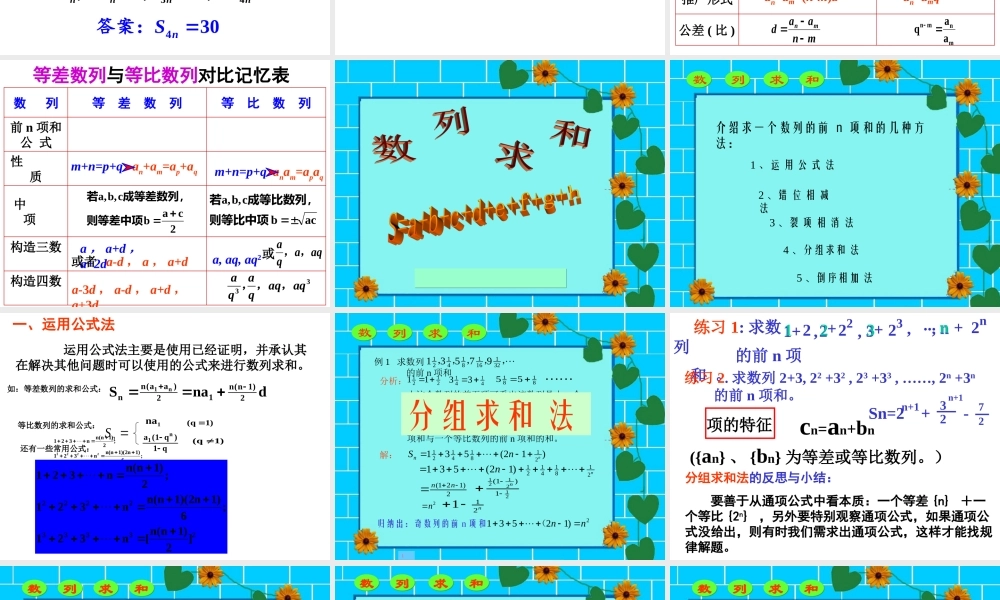
111(1)(1)111nnnnaqnSqqaaSqqq等比数列的前项和这个公式还可以写成1=,1nnakSkkqq如果设那么这个式子说明什么问题呢？nnnSkkqqq说明的系数与常数项是的，其中的互为相反数就是公比233,2nnnanSkkq等比数列的前项和很容易得出：公比性质一2322,,,mmmmmSSSSSdmd我们知道，在中有以下性质：也成等差等差数列数列公差请把这条性质经过类比，推广到等比数列232,,,,nnmmmmmanSSSSSS等比数列设的前项和为则有：也成等比数列证明这个结论！性质二3070S答案：51162ma答案：，10203010,=30naSSS例1.等比数列中，，求5.31,nnnanSmma例2等比数列的前项和求的值以及的值.110103020101.,2,2(21)0..nnnaanSSSSa例3设正项等比数列首项前项和为且求的通项公式34,2,14,nnnnnanSSSS练习：各项均为正的等比数列的前项和为若求1()2nna答案：430nS答案：等差数列等比数列定义一般地,如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫做等差数列．这个常数叫公差．一般地，如果一个数列从第2项起，每一项与它的前一项的比等于同一个常数，那么这个数列就叫等比数列．这个常数叫公比．等差数列与等比数列对比记忆表数列等差数列等比数列定义式公差（比）通项公式推广形式公差(比)an+1-an=dd叫公差q叫公比an=a1+(n-1)dan=a1qn-1an=am+(n-m)dan=amqn-mmnaadmnmnmnaaqqaa1nn等差数列与等比数列对比记忆表数列等差数列等比数列前n项和公式性质中项构造三数构造四数a，a+d，a+2da,aq,aq2或者a-d，a，a+daqaqa，，或a-3d，a-d，a+d，a+3d33aqaqqaqa，，，m+n=p+qan+am=ap+aqm+n=p+qanam=apaq2cabcb,a,则等差中项成等差数列，若acbcb,a,则等比中项成等比数列，若等差数列与等比数列对比记忆表数列求和介绍求一个数列的前n项和的几种方法：1、运用公式法2、错位相减法3、裂项相消法4、分组求和法5、倒序相加法一、运用公式法运用公式法主要是使用已经证明，并承认其在解决其他问题时可以使用的公式来进行数列求和。如：等差数列的求和公式：dnaS2)1n(n12)aa(nnn1等比数列的求和公式：nS1naq1)q1(an1)1q()1q(还有一些常用公式：233332222]2)1n(n[n321;6)1n2)(1n(nn321;2)1n(nn321233332222]2)1n(n[n321;6)1n2)(1n(nn321;2)1n(nn32...