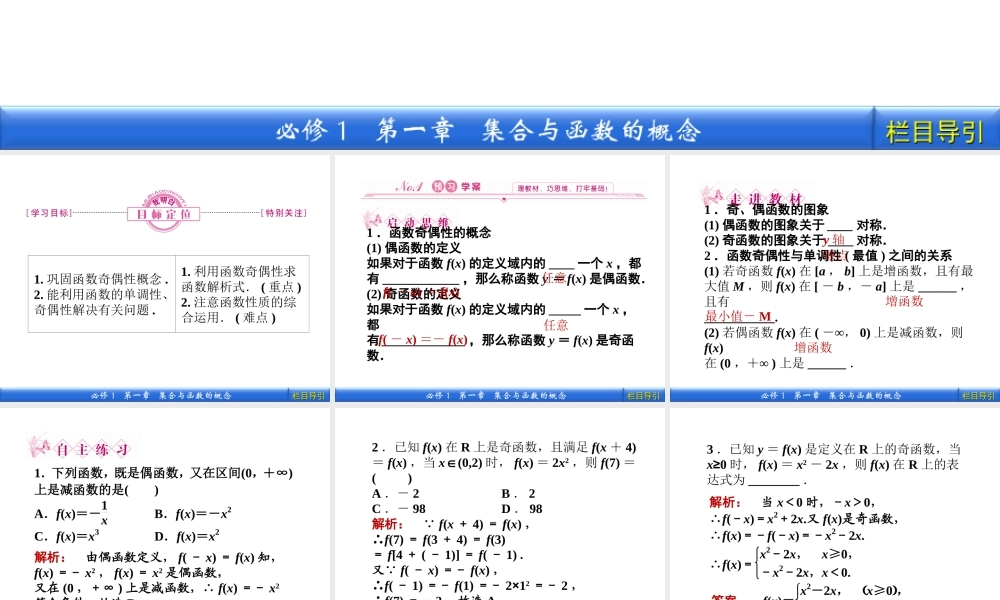
栏目导引栏目导引必修1第一章集合与函数的概念第2课时函数奇偶性的应用栏目导引栏目导引必修1第一章集合与函数的概念1.巩固函数奇偶性概念.2.能利用函数的单调性、奇偶性解决有关问题.1.利用函数奇偶性求函数解析式.(重点)2.注意函数性质的综合运用.(难点)栏目导引栏目导引必修1第一章集合与函数的概念1.函数奇偶性的概念(1)偶函数的定义如果对于函数f(x)的定义域内的____一个x,都有____________,那么称函数y=f(x)是偶函数.(2)奇函数的定义如果对于函数f(x)的定义域内的_____一个x,都有_____________,那么称函数y=f(x)是奇函数.f(-x)=f(x)f(-x)=-f(x)任意任意栏目导引栏目导引必修1第一章集合与函数的概念1.奇、偶函数的图象(1)偶函数的图象关于____对称.(2)奇函数的图象关于____对称.2.函数奇偶性与单调性(最值)之间的关系(1)若奇函数f(x)在[a,b]上是增函数,且有最大值M,则f(x)在[-b,-a]上是______,且有___________.(2)若偶函数f(x)在(-∞,0)上是减函数,则f(x)在(0,+∞)上是______.y轴原点增函数最小值-M增函数栏目导引栏目导引必修1第一章集合与函数的概念1.下列函数,既是偶函数,又在区间(0,+∞)上是减函数的是()A.f(x)=-1xB.f(x)=-x2C.f(x)=x3D.f(x)=x2解析:由偶函数定义,f(-x)=f(x)知,f(x)=-x2,f(x)=x2是偶函数,又在(0,+∞)上是减函数,∴f(x)=-x2符合条件,故选B.答案:B栏目导引栏目导引必修1第一章集合与函数的概念2.已知f(x)在R上是奇函数,且满足f(x+4)=f(x),当x∈(0,2)时,f(x)=2x2,则f(7)=()A.-2B.2C.-98D.98解析: f(x+4)=f(x),∴f(7)=f(3+4)=f(3)=f[4+(-1)]=f(-1).又 f(-x)=-f(x),∴f(-1)=-f(1)=-2×12=-2,∴f(7)=-2,故选A.答案:A栏目导引栏目导引必修1第一章集合与函数的概念3.已知y=f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-2x,则f(x)在R上的表达式为________.解析:当x<0时,-x>0,∴f(-x)=x2+2x.又f(x)是奇函数,∴f(x)=-f(-x)=-x2-2x.∴f(x)=x2-2x,x≥0,-x2-2x,x<0.答案:f(x)=x2-2x,x≥0,-x2-2x,x<0.栏目导引栏目导引必修1第一章集合与函数的概念4.函数y=f(x)是偶函数,且在(-∞,0]上为增函数,试比较f(-2)与f(1)的大小.解析: f(x)是偶函数,∴f(1)=f(-1)又 f(x)在(-∞,0]上为增函数,-2<-1∴f(-2)<f(-1)=f(1)即f(-2)<f(1)栏目...