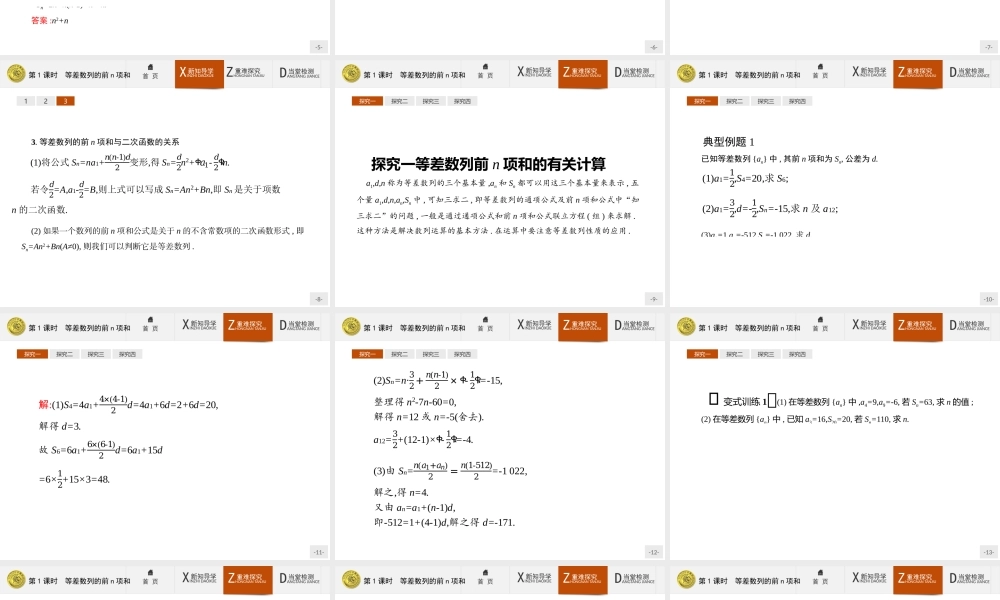
-1-2.3等差数列的前n项和-2-第1课时等差数列的前n项和-3-第1课时等差数列的前n项和首页XINZHIDAOXUE新知导学ZHONGNANTANJIU重难探究DANGTANGJIANCE当堂检测学习目标思维脉络1.理解等差数列前n项和公式的推导方法——倒序相加法.2.掌握等差数列前n项和公式,掌握等差数列五个量a1,n,d,an,Sn之间的关系.3.掌握由Sn求an的方法.4.理解前n项和与二次函数的关系.-4-第1课时等差数列的前n项和XINZHIDAOXUE新知导学首页ZHONGNANTANJIU重难探究DANGTANGJIANCE当堂检测1231.数列的前n项和对于数列{an},一般地,我们称a1+a2+a3+…+an为数列{an}的前n项和,用Sn表示,即Sn=a1+a2+a3+…+an.练一练1已知数列{an}的通项公式an=n2+1,若其前n项和为Sn,则S3=.解析: an=n2+1,∴a1=2,a2=5,a3=10,∴S3=a1+a2+a3=17.答案:17-5-第1课时等差数列的前n项和XINZHIDAOXUE新知导学首页ZHONGNANTANJIU重难探究DANGTANGJIANCE当堂检测1232.等差数列{an}的前n项和设等差数列{an}的公差是d,则练一练2已知数列{an}为等差数列,首项a1=2,公差d=2,则其前n项和Sn=.∴Sn=2n+n(n-1)=n2+n.答案:n2+nSn=𝑛(𝑎1+𝑎𝑛)2=na1+𝑛(𝑛-1)2d.解析: Sn=na1+𝑛(𝑛-1)𝑑2,-6-第1课时等差数列的前n项和XINZHIDAOXUE新知导学首页ZHONGNANTANJIU重难探究DANGTANGJIANCE当堂检测123练一练3已知数列{an}为等差数列,a1=2,an=10,Sn=72,则n=.答案:12解析: Sn=𝑛(𝑎1+𝑎𝑛)2,∴𝑛(2+10)2=72,得n=12.-7-第1课时等差数列的前n项和XINZHIDAOXUE新知导学首页ZHONGNANTANJIU重难探究DANGTANGJIANCE当堂检测123名师点拨1.当已知首项a1、末项an、项数n时,常用公式当已知首项a1、公差d、项数n时,常用公式2.等差数列前n项和公式的推导方法“倒序相加法”,是解决数列求和问题的一种重要方法,主要适用于具有a1+an=a2+an-1=a3+an-2=…特征的数列求和.Sn=𝑛(𝑎1+𝑎𝑛)2;Sn=na1+𝑛(𝑛-1)2d.-8-第1课时等差数列的前n项和XINZHIDAOXUE新知导学首页ZHONGNANTANJIU重难探究DANGTANGJIANCE当堂检测1233.等差数列的前n项和与二次函数的关系(2)如果一个数列的前n项和公式是关于n的不含常数项的二次函数形式,即Sn=An2+Bn(A≠0),则我们可以判断它是等差数列.(1)将公式Sn=na1+𝑛(𝑛-1)𝑑2变形,得Sn=𝑑2n2+ቀ𝑎1-𝑑2ቁn.若令𝑑2=A,a1-𝑑2=B,则上式可以写成Sn=An2+Bn,即Sn是关于项数n的二次函数.-9-第1课时等差数列的前n项和ZHONGNANTANJIU重难探究首页XINZHIDAOXUE新知导学DANGTANGJIANCE当堂检测探究一探究二探究三探究四探究一等差数列前n...