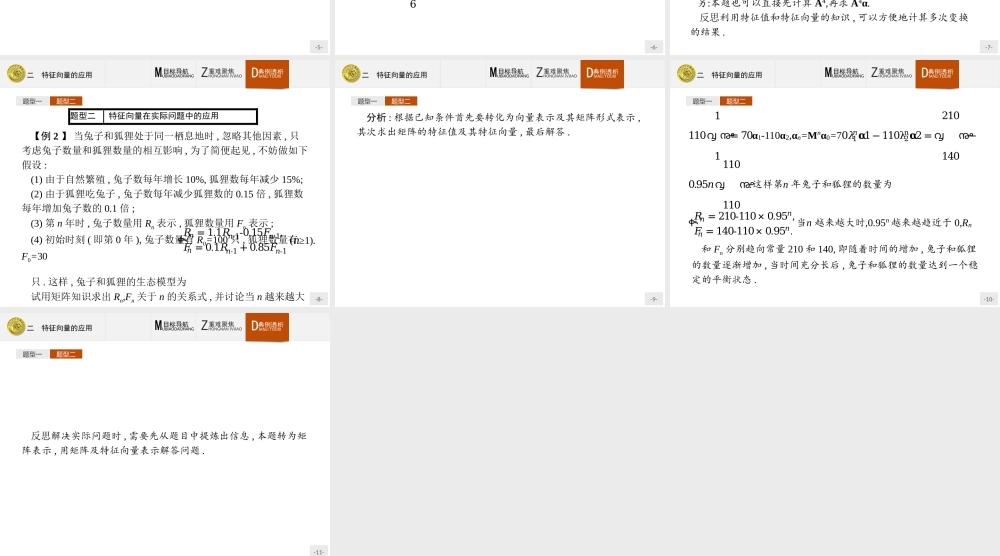
-1-二特征向量的应用-2-二特征向量的应用ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航1.利用矩阵A的特征值、特征向量给出Anα的简单的表示,并能用它来解决问题.2.会利用特征向量解决简单的实际问题.-3-二特征向量的应用ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航1.设二阶矩阵A的两个特征值λ1,λ2对应的两个特征向量分别为ξ1,ξ2,σ为二阶矩阵A对应的线性变换,α为平面内的任意一个向量,那么Anα(n∈N*)能否用ξ1和ξ2表示出来呢?剖析:因为ξ1,ξ2是二阶矩阵A的两个特征向量,所以ξ1,ξ2不共线,则平面内的任意一个向量α就可以用ξ1,ξ2表示出来,即存在实数t1,t2使得α=t1ξ1+t2ξ2,Aξ1=λ1ξ1,Aξ2=λ2ξ2.所以σα=Aα=A(t1ξ1+t2ξ2)=t1(Aξ1)+t2(Aξ2)=t1λ1ξ1+t2λ2ξ2,σ2α=A2α=A(Aα)=A(t1λ1ξ1+t2λ2ξ2)=t1λ1(Aξ1)+t2λ2(Aξ2)=t1𝜆12𝛏1+𝑡2𝜆22𝛏2,σ3α=A3α=A(A2α)=A(t1𝜆12𝛏1+𝑡2𝜆22𝛏2)=𝑡1𝜆12(Aξ1)+t2𝜆22(Aξ2)=t1𝜆13𝛏1+𝑡2𝜆23𝛏2,……σnα=Anα=t1𝜆1𝑛𝛏1+𝑡2𝜆2𝑛𝛏2.-4-二特征向量的应用ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航2.求Anα的基本步骤是什么?剖析:第一步:由特征向量的定义Aξ=λξ,求出特征值λ和相应的特征向量ξ;第二步:把向量α改写为用ξ1和ξ2表示,即α=t1ξ1+t2ξ2;第三步:由性质公式计算Anα=t1𝜆1𝑛𝛏1+𝑡2𝜆2𝑛𝛏2.-5-二特征向量的应用ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航题型一题型二题型一Anα的简单表示【例1】已知矩阵A=ۉۈۇ8-56-3یۋۊ,向量𝛂=൮78൲,求A4α.分析:求出A的特征值及相应的特征向量,代入公式求解即可.-6-二特征向量的应用ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航题型一题型二解: 矩阵A的特征值满足方程ቤ𝜆-85-6𝜆+3ቤ=0,∴(λ-8)(λ+3)+30=0,得λ1=2,λ2=3.当λ1=2时,ቊ(2-8)𝑥+5𝑦=0,-6𝑥+5𝑦=0,得一组非零解൮56൲,∴ξ1=൮56൲是λ1=2的一个特征向量.-7-二特征向量的应用ZHONGNANJVJIAO重难聚焦DIANLITOUXI典例透析MUBIAODAOHANG目标导航同理可求得ξ2=൮11൲是λ2=3的一个特征向量.又α=൮78൲=൮56൲+2൮11൲,∴A4α=𝜆14൮56൲+2𝜆24൮11൲=24൮56൲+2×34൮11൲=൮242258൲.另:本题也可以直接先计算A4,再求A4α.题型一题型二反思利用特征值和特征向量的知识,可以方便地计算多次变换的结果.-8-二特征向量的应用ZHONGNANJVJIAO...