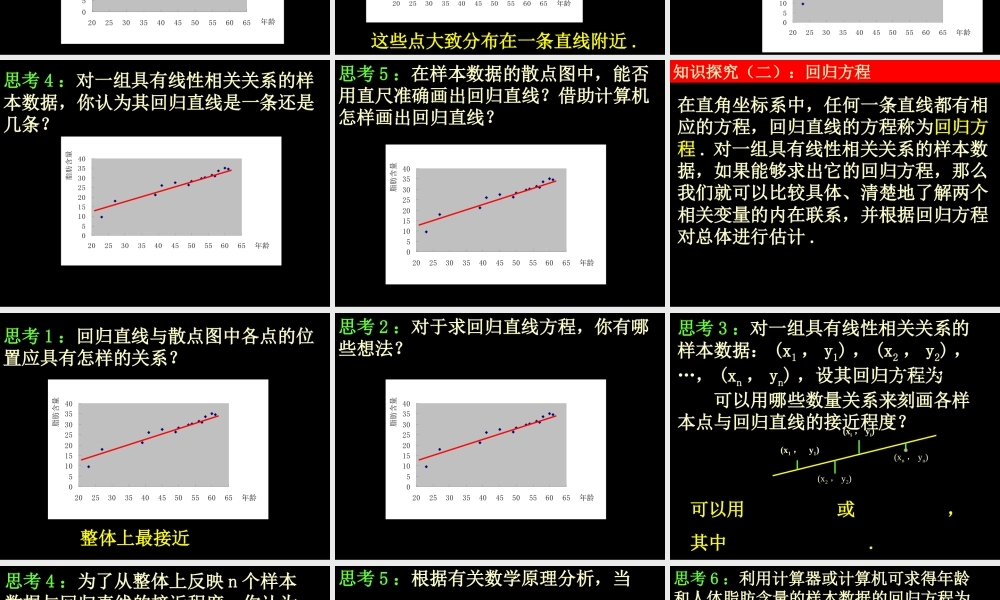
2.3变量间的相关关系2.3.1变量之间的相关关系2.3.2两个变量的线性相关第二课时问题提出1.两个变量之间的相关关系的含义如何?成正相关和负相关的两个相关变量的散点图分别有什么特点?自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系.正相关的散点图中的点散布在从左下角到右上角的区域,负相关的散点图中的点散布在从左上角到右下角的区域2.观察人体的脂肪含量百分比和年龄的样本数据的散点图,这两个相关变量成正相关.我们需要进一步考虑的问题是,当人的年龄增加时,体内脂肪含量到底是以什么方式增加呢?对此,我们从理论上作些研究.051015202530354020253035404550556065年龄脂肪含量知识探究(一):回归直线思考1:一组样本数据的平均数是样本数据的中心,那么散点图中样本点的中心如何确定?它一定是散点图中的点吗?051015202530354020253035404550556065年龄脂肪含量(,)xy思考2:在各种各样的散点图中,有些散点图中的点是杂乱分布的,有些散点图中的点的分布有一定的规律性,年龄和人体脂肪含量的样本数据的散点图中的点的分布有什么特点?051015202530354020253035404550556065年龄脂肪含量这些点大致分布在一条直线附近.思考3:如果散点图中的点的分布,从整体上看大致在一条直线附近,则称这两个变量之间具有线性相关关系,这条直线叫做回归直线.对具有线性相关关系的两个变量,其回归直线一定通过样本点的中心吗?051015202530354020253035404550556065年龄脂肪含量思考4:对一组具有线性相关关系的样本数据,你认为其回归直线是一条还是几条?051015202530354020253035404550556065年龄脂肪含量思考5:在样本数据的散点图中,能否用直尺准确画出回归直线?借助计算机怎样画出回归直线?051015202530354020253035404550556065年龄脂肪含量知识探究(二):回归方程在直角坐标系中,任何一条直线都有相应的方程,回归直线的方程称为回归方程.对一组具有线性相关关系的样本数据,如果能够求出它的回归方程,那么我们就可以比较具体、清楚地了解两个相关变量的内在联系,并根据回归方程对总体进行估计.思考1:回归直线与散点图中各点的位置应具有怎样的关系?整体上最接近051015202530354020253035404550556065年龄脂肪含量思考2:对于求回归直线方程,你有哪些想法?051015202530354020253035404550556065年龄脂肪含量(x1,y1)(x2,y2)(xi,yi)(xn,yn)可以用或,其中.思考3:对一组具有线性相关关系的样本数据:(...