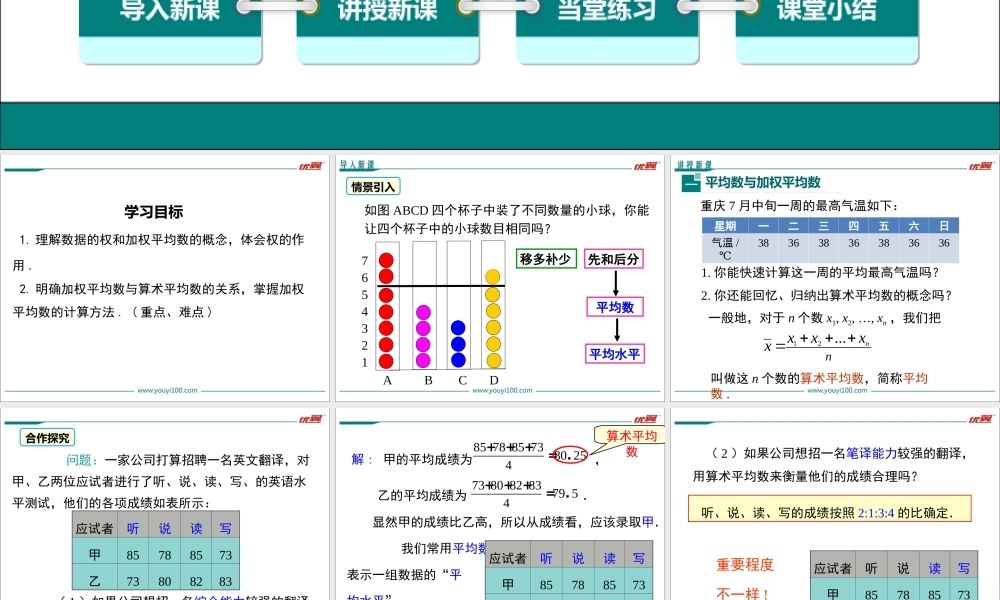
20.1.1平均数第二十章数据的分析优翼课件导入新课讲授新课当堂练习课堂小结学练优八年级数学下(RJ)教学课件第1课时平均数和加权平均数情境引入学习目标1.理解数据的权和加权平均数的概念,体会权的作用.2.明确加权平均数与算术平均数的关系,掌握加权平均数的计算方法.(重点、难点)7654321ABCD平均数先和后分移多补少如图ABCD四个杯子中装了不同数量的小球,你能让四个杯子中的小球数目相同吗?平均水平导入新课情景引入重庆7月中旬一周的最高气温如下:星期一二三四五六日气温/℃383638363836361.你能快速计算这一周的平均最高气温吗?2.你还能回忆、归纳出算术平均数的概念吗?一般地,对于n个数x1,x2,…,xn,我们把12...nnxxxx叫做这n个数的算术平均数,简称平均数.讲授新课平均数与加权平均数一问题:一家公司打算招聘一名英文翻译,对甲、乙两位应试者进行了听、说、读、写、的英语水平测试,他们的各项成绩如表所示:(1)如果公司想招一名综合能力较强的翻译,请计算两名应试者的平均成绩,应该录用谁?应试者听说读写甲85788573乙73808283合作探究乙的平均成绩为.738082837954+++=.显然甲的成绩比乙高,所以从成绩看,应该录取甲.我们常用平均数表示一组数据的“平均水平”.应试者听说读写甲85788573乙73808283解:甲的平均成绩为,8578857380254+++=.算术平均数(2)如果公司想招一名笔译能力较强的翻译,用算术平均数来衡量他们的成绩合理吗?应试者听说读写甲85788573乙73808283听、说、读、写的成绩按照2:1:3:4的比确定.重要程度不一样!应试者听说读写甲85788573乙738082832:1:3:47328018238348042134+++==..+++x乙因为乙的成绩比甲高,所以应该录取乙.8527818537347952134+++==.+++x甲解:,4312权思考:能把这种加权平均数的计算方法推广到一般吗?8578857213421379345+++=.+++112212+++=+++nnnxwxwxwxwww一般地,若n个数x1,x2,…,xn的权分别是w1,w2,…,wn,则叫做这n个数的加权平均数.归纳(3)如果公司想招一名口语能力较强的翻译,则应该录取谁?应试者听说读写甲85788573乙73808283听、说、读、写的成绩按照3:3:2:2的比确定.同样一张应试者的应聘成绩单,由于各个数据所赋的权数不同,造成的录取结果截然不同.(4)将问题(1)、(2)、(3)比较,你能体会到权的作用吗?应试者听说读写甲85788573乙73808283数据的权能够反映数据的相对重要程度!例1一次演讲比赛中,评委将从...