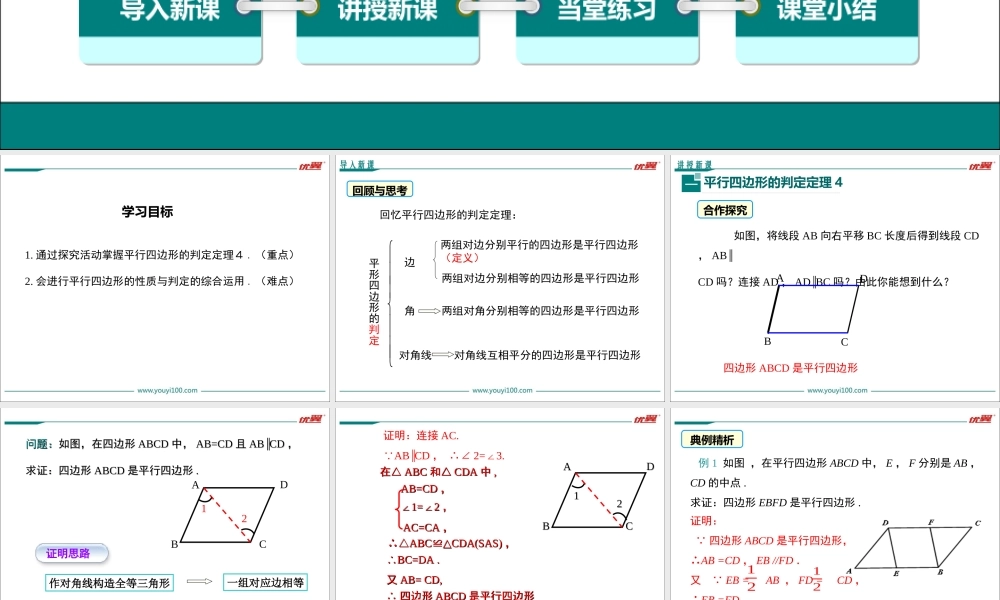
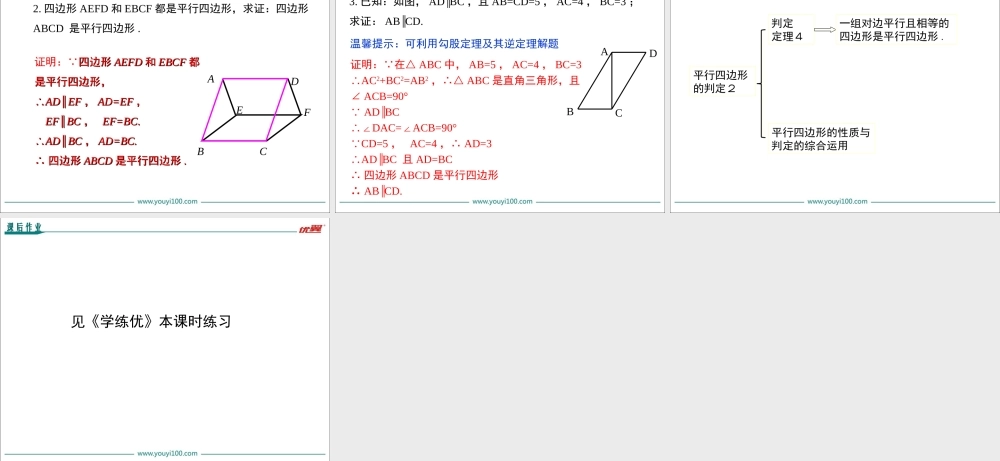
18.1.2平行四边形判定第十八章平行四边形优翼课件导入新课讲授新课当堂练习课堂小结学练优八年级数学下(RJ)教学课件第2课时平行四边形的判定(2)情境引入学习目标1.通过探究活动掌握平行四边形的判定定理4.(重点)2.会进行平行四边形的性质与判定的综合运用.(难点)导入新课回忆平行四边形的判定定理:平形四边形的判定两组对边分别平行的四边形是平行四边形(定义)边两组对边分别相等的四边形是平行四边形两组对角分别相等的四边形是平行四边形对角线互相平分的四边形是平行四边形角对角线回顾与思考讲授新课平行四边形的判定定理4一合作探究BA如图,将线段AB向右平移BC长度后得到线段CD,AB∥CD吗?连接AD,AD∥BC吗?由此你能想到什么?DC四边形ABCD是平行四边形ABCD21证明思路作对角线构造全等三角形一组对应边相等两组对边分别相等四边形ABCD是平行四边形问题:问题:如图,在四边形如图,在四边形ABCDABCD中,中,AB=CDAB=CD且且ABAB∥∥CDCD,,求证:四边形求证:四边形ABCDABCD是平行四边形是平行四边形..一组对边平行且相等的四边形是平行四边形.定理AABBCCDD2211证明:连接AC. AB∥CD,∴∠2=3.∠在△在△ABCABC和△和△CDACDA中中,,AB=CDAB=CD,,AC=CAAC=CA,,∠∠1=2∠1=2∠,,∴△∴△ABCABC≌≌CDA(SAS)△CDA(SAS)△,,∴∴BC=DABC=DA..又又AB=CD,AB=CD,∴∴四边形四边形ABCDABCD是平行四边形是平行四边形..典例精析证明: 四边形ABCD是平行四边形,∴AB=CD,EB//FD.又 EB=AB,FD=CD,∴EB=FD.∴四边形EBFD是平行四边形.1212例1如图,在平行四边形ABCD中,E,F分别是AB,CD的中点.求证:四边形EBFD是平行四边形.如图,在平行四边形ABCD中,E、F分别是边AB、CD的中点,四边形AEFD是平行四边形吗?为什么?解:四边形AEFD是平行四边形.理由如下: 四边形ABCD是平行四边形,∴AB∥DC,AB=DC.又 E、F分别是边AB、CD的中点,∴AE=DF.又 AE∥DF,∴四边形AEFD是平行四边形.练一练为了保证铁路的两条直铺的铁轨互相平行,只要使互相平行的夹在铁轨之间的枕木长相等就可以了.你能说出其中的道理吗?贴上图片学以致用平行四边形的性质与判定的综合运用二例2如图,在ABCD中,AEBD⊥于E,CFBD⊥于F,连接AF,CE.求证:AF=CE.证明: 四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠ABE=CDF∠.分析:证AF=CE只需证四边形AECF是平行四边形.由AEBD⊥,CFBD⊥得AE∥CF.通过证△ABE≌CDF△,得AE=CF,结论...