17.2 第1课时 勾股定理的逆定理1.pptVIP免费

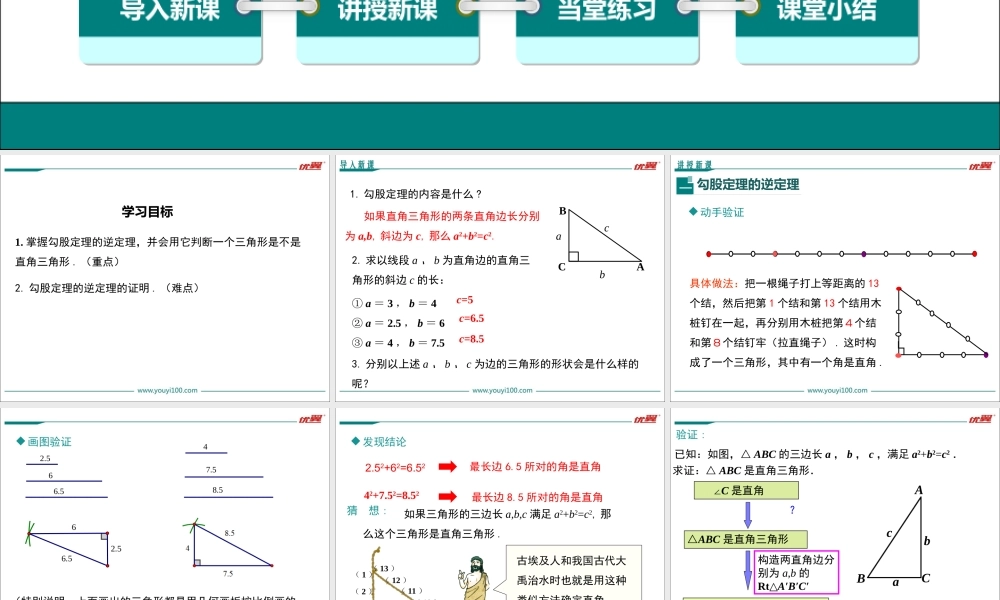
17.2勾股定理的逆定理第十七章勾股定理优翼课件导入新课讲授新课当堂练习课堂小结学练优八年级数学下（RJ）教学课件第1课时勾股定理的逆定理情境引入学习目标1.掌握勾股定理的逆定理，并会用它判断一个三角形是不是直角三角形.（重点）2.勾股定理的逆定理的证明.（难点）导入新课BCA1.勾股定理的内容是什么?如果直角三角形的两条直角边长分别为a,b,斜边为c,那么a2+b2=c2.bca2.求以线段a、b为直角边的直角三角形的斜边c的长：①a＝3，b＝4②a＝2.5，b＝6③a＝4，b＝7.5c=5c=6.5c=8.53.分别以上述a、b、c为边的三角形的形状会是什么样的呢？讲授新课一勾股定理的逆定理具体做法：把一根绳子打上等距离的13个结，然后把第1个结和第13个结用木桩钉在一起，再分别用木桩把第４个结和第８个结钉牢（拉直绳子）.这时构成了一个三角形，其中有一个角是直角.动手验证画图验证6.562.56.562.58.57.54（特别说明，上面画出的三角形都是用几何画板按比例画的，结果也都是直角三角形）.发现结论2.52+62=6.5242+7.52=8.52最长边6.5所对的角是直角最长边8.5所对的角是直角（1）（2）（3）（4）（5）（6）（7）（8）（13）（12）（11）（10）（9）古埃及人和我国古代大禹治水时也就是用这种类似方法确定直角.如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.猜想:△ABC≌△A′B′C′？∠C是直角△ABC是直角三角形ABCabc已知：如图，△ABC的三边长a，b，c，满足a2+b2=c2．求证：△ABC是直角三角形．构造两直角边分别为a,b的Rt△A′B′C′验证:证明：作Rt△A′B′C′，使∠C′=900，A′C′=b，B′C′=a△ABC≌△A′B′C′(SSS)∴∠C=∠C′=900即△ABC是直角三角形.则22222ABBCACab222abc22ABcABc在和中ABCABCACACBCBCABABCBaAbcACaBbc勾股定理的逆定理归纳总结如果三角形的三边长a、b、c满足a2+b2=c2那么这个三角形是直角三角形.ACBabc勾股定理的逆定理是直角三角形的判定定理，即已知三角形的三边长，且满足两条较小边的平方和等于最长边的平方，即可判断此三角形为直角三角，最长边所对角为直角.特别说明：典例精析例1下面以a,b,c为边长的三角形是不是直角三角形？如果是,那么哪一个角是直角？(1)a=15，b=8，c=17;解：因为152+82=289，172=289，所以152+82=172，根据勾股定理的逆定理，这个三角形是直角三角形，且∠C是直角.(2)a=13，b=14，c=15...