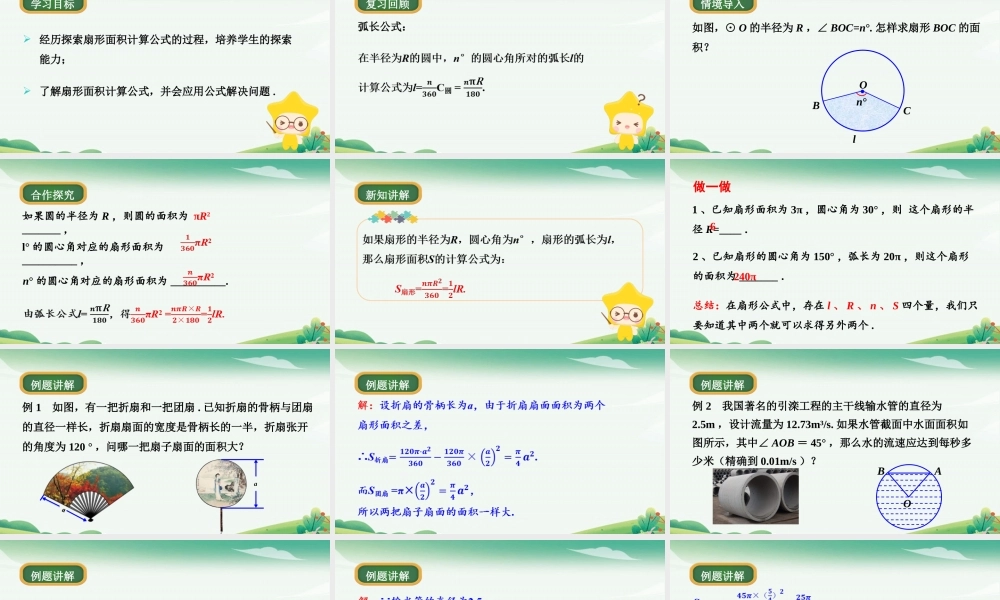
第2课时扇形面积的计算经历探索扇形面积计算公式的过程,培养学生的探索能力;学习目标了解扇形面积计算公式,并会应用公式解决问题.复习回顾弧长公式:如图,⊙O的半径为R,∠BOC=n°.怎样求扇形BOC的面积?情境导入BOCln°n°的圆心角对应的扇形面积为__________.如果圆的半径为R,则圆的面积为_______,l°的圆心角对应的扇形面积为__________,合作探究πR2新知讲解做一做1、已知扇形面积为3π,圆心角为30°,则这个扇形的半径R=____.2、已知扇形的圆心角为150°,弧长为20π,则这个扇形的面积为_______.6240π总结:在扇形公式中,存在l、R、n、S四个量,我们只要知道其中两个就可以求得另外两个.例1如图,有一把折扇和一把团扇.已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120°,问哪一把扇子扇面的面积大?例题讲解aa例题讲解例2我国著名的引滦工程的主干线输水管的直径为2.5m,设计流量为12.73m³/s.如果水管截面中水面面积如图所示,其中∠AOB=45°,那么水的流速应达到每秒多少米(精确到0.01m/s)?例题讲解OBA分析:由图,不难发现截面中有水部分(阴影部分)的面积是圆的面积与空隙部分(弓形)面积之差.因此根据水的流量、截面中水面面积与流速的关系,即可求得水的流速.例题讲解例题讲解例题讲解(1)通过“割”“补”“拼”“凑”等方法将不规则图形的面积转化为几个规则图形面积的和或差的形式.求不规则图形面积的常用策略规律总结(2)通过等积代换的方法将不规则图形的面积转化成规则图形的面积.1、扇形的面积大小()A、只与半径长短有关B、只与圆心角大小有关C、与圆心角的大小、半径的长短有关C随堂练习B随堂练习3、如图,方格纸中4个小正方形的边长均为1,则图中阴影部分三个小扇形的面积和为______(结果保留π).随堂练习OABCDE随堂练习OABCD随堂练习求不规则图形的面积时,先通过割补将其规则化,再按相应的公式来求解.E1、如果扇形的半径为R,圆心角为n°,那么扇形面积的计算公式为S扇形=_______.2、用弧长来表示扇形的面积:3、求不规则图形的面积的常用策略:用“割”“补”“拼”“凑”或等积代换的方法转化为规则图形面积的形式.课堂小结感谢观看!