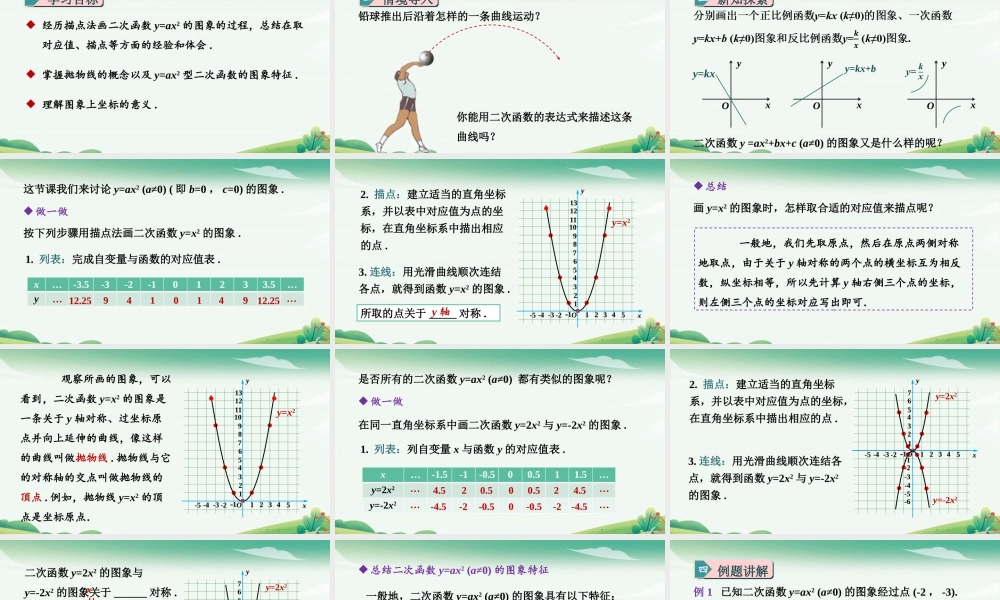
1.2二次函数的图象第1课时二次函数y=ax2的图象学习目标一经历描点法画二次函数y=ax2的图象的过程,总结在取对应值、描点等方面的经验和体会.掌握抛物线的概念以及y=ax2型二次函数的图象特征.理解图象上坐标的意义.情境导入二铅球推出后沿着怎样的一条曲线运动?你能用二次函数的表达式来描述这条曲线吗?新知探索三xyOy=kxxyOy=kx+bxyO二次函数y=ax2+bx+c(a≠0)的图象又是什么样的呢?x…-3.5-3-2-101233.5…y这节课我们来讨论y=ax2(a≠0)(即b=0,c=0)的图象.做一做按下列步骤用描点法画二次函数y=x2的图象.1.列表:完成自变量与函数的对应值表.014914912.2512.25……3.连线:用光滑曲线顺次连结各点,就得到函数y=x2的图象.2.描点:建立适当的直角坐标系,并以表中对应值为点的坐标,在直角坐标系中描出相应的点.12345x12345678910yO-1-2-3-4-5111213y=x2所取的点关于_____对称.y轴画y=x2的图象时,怎样取合适的对应值来描点呢?一般地,我们先取原点,然后在原点两侧对称地取点,由于关于y轴对称的两个点的横坐标互为相反数,纵坐标相等,所以先计算y轴右侧三个点的坐标,则左侧三个点的坐标对应写出即可.总结观察所画的图象,可以看到,二次函数y=x2的图象是一条关于y轴对称、过坐标原点并向上延伸的曲线,像这样的曲线叫做抛物线.抛物线与它的对称轴的交点叫做抛物线的顶点.例如,抛物线y=x2的顶点是坐标原点.12345x12345678910yO-1-2-3-4-5111213y=x2是否所有的二次函数y=ax2(a≠0)都有类似的图象呢?做一做在同一直角坐标系中画二次函数y=2x2与y=-2x2的图象.1.列表:列自变量x与函数y的对应值表.x…-1.5-1-0.500.511.5…y=2x2y=-2x200.524.50.524.5……0-0.5-2-4.5-0.5-2-4.5……3.连线:用光滑曲线顺次连结各点,就得到函数y=2x2与y=-2x2的图象.2.描点:建立适当的直角坐标系,并以表中对应值为点的坐标,在直角坐标系中描出相应的点.12345x-5-4-3-2-11234yO-1-2-3-4-5567-6y=2x2y=-2x212345x-5-4-3-2-11234yO-1-2-3-4-5567-6二次函数y=2x2的图象与y=-2x2的图象关于______对称.如果已知y=ax2(a≠0)的图象,可通过_________更方便地得到y=-ax2的图象.当a>0时,抛物线开口向___;当a<0时,抛物线开口向x轴翻折上下y=2x2y=-2x2总结二次函数y=ax2(a≠0)的图象特征二次函数y=ax2(a≠0)的图象是一条抛物线,它关于y轴对称,顶点是坐标原点.当a>0时,抛物线的开口向上,顶点是抛物线的最___点;当a<0时,抛物线的开口向下,顶点...