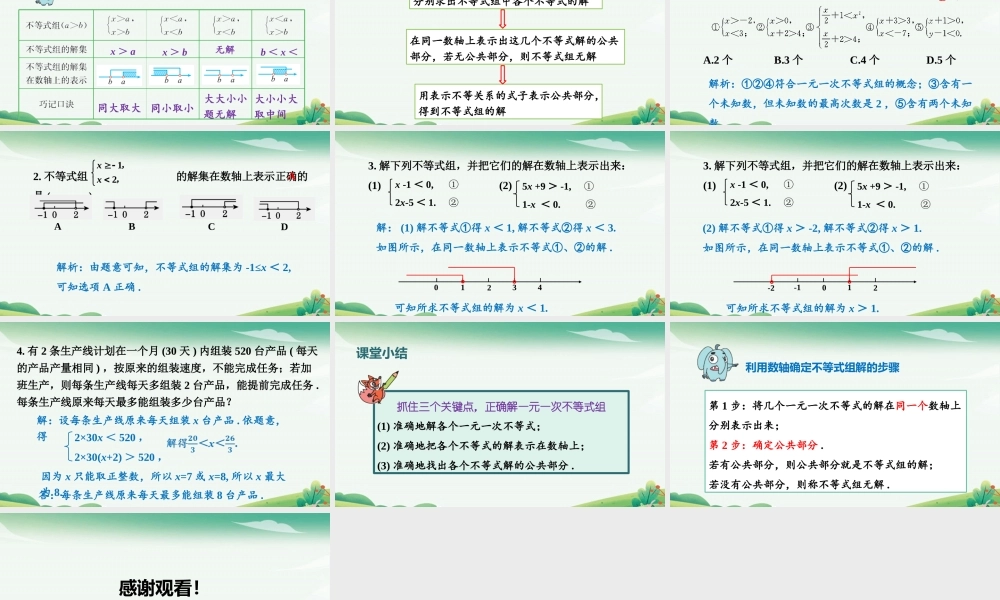
第3章一元一次不等式3.4一元一次不等式组学习目标1.理解一元一次不等式组的概念.2.理解不等式组的解的概念.3.会解由两个一元一次不等式组成的不等式组,并会用数轴确定解.合作探究一个长方形足球训练场的长为x(m),宽为70m.如果它的周长大于350m,面积小于7560m2,你能确定x的取值范围吗?在现实生活中,我们会遇到一个未知数需要同时满足若干个不等式的情况.如:根据这个问题,小组讨论,能够列出什么式子?一个长方形足球训练场的长为x(m),宽为70m.如果它的周长大于350m,面积小于7560m2,你能确定x的取值范围吗?针对这个问题,我们可以列出两个不等式:2(x+70)>350,70x<7560.2(x+70)>350,70x<7560.一般地,由几个含同一未知数的一元一次不等式所组成的一组不等式,叫做一元一次不等式组.例如,3x-2>1-2x,x≥0,都是一元一次不等式组.新知讲解组成不等式组的各个不等式的解的公共部分就是不等式组的解.当它们没有公共部分时,我们称这个不等式组无解.思考:如何确定不等式解的公共部分呢?数轴是确定一元一次不等式组的解的有效工具,可以利用数轴表示各个不等式的解,从而得到不等式组的解.例题解答例1解一元一次不等式组分析:根据一元一次不等式组的解的意义,我们只要分别求出①,②两个不等式的解,并把解表示在同一条数轴上,两个不等式的解的公共部分即为不等式组的解.例题解答例1解一元一次不等式组解:解不等式①,得x>-1.解不等式②,得x≤6.把①,②两个不等式的解表示在数轴上,如图所示:所以原不等式组的解是-1<x≤6.-3-2-101234567例2解一元一次不等式组-3-2-101234567所以原不等式组无解.一元一次不等式组解的四种情况x>ax>b无解b<x<a同大取大同小取小大大小小题无解大小小大取中间归纳小结解一元一次不等式组的步骤分别求出不等式组中各个不等式的解在同一数轴上表示出这几个不等式解的公共部分,若无公共部分,则不等式组无解用表示不等关系的式子表示公共部分,得到不等式组的解随堂练习1.下列不等式组,其中是一元一次不等式组的有()A.2个B.3个C.4个D.5个解析:①②④符合一元一次不等式组的概念;③含有一个未知数,但未知数的最高次数是2,⑤含有两个未知数B2.不等式组的解集在数轴上表示正确的是()12xx,,ABCD解析:由题意可知,不等式组的解集为-1≤x<2,可知选项A正确.A3.解下列不等式组,并把它们的解在数轴上表示出来:(1)(2)x-1<0,①2x-5<1.②5x+9>-1,①1-x<0.②解:(1)解不等式①得x<...