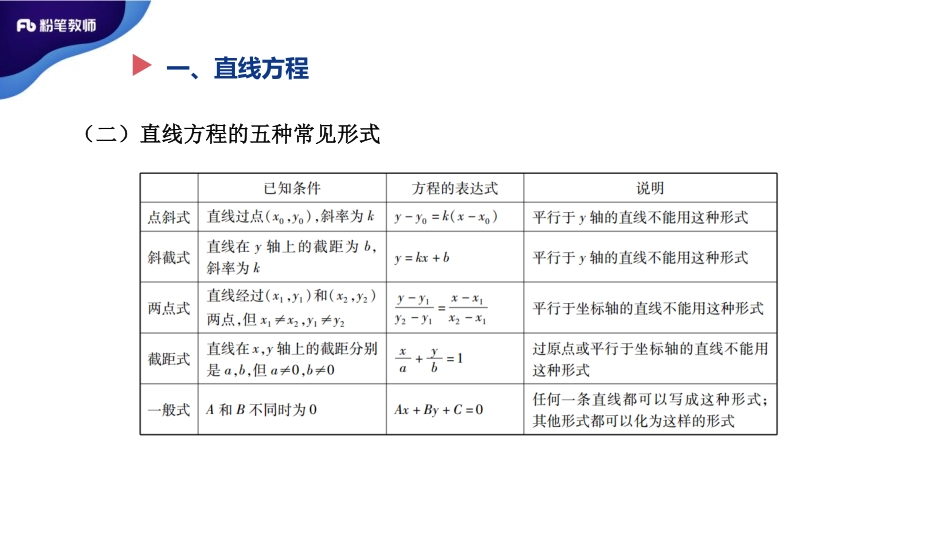
2020教师招聘理论精讲图形与几何2主讲:吴倩一、直线方程(二)直线方程的五种常见形式一、直线方程(三)点到直线的距离已知点(x0,y0)与直线Ax+By+C=0,d=𝐴𝑥0+𝐵𝑦0+𝐶𝐴2+𝐵2(四)平行线间距离若l1:Ax+By+C1=0,l2:Ax+By+C2=0平行,d=𝐶1−𝐶2𝐴2+𝐵2一、直线方程(五)直线的位置关系当直线方程为l1:y=k1x+b1,l2:y=k2x+b2时,位置关系结论l1∥l2k1=k2且b1≠b2l1⊥l2k1▪k2=-1检验下听课效果2.已知直线l1:ax-y+2a=0,l2:(2a-1)x+ay+a=0互相垂直,则实常数a的值是()A.0B.1C.0或1D.0或-1二、圆的方程检验下听课效果3.方程𝑥−2=4−𝑦2表示的曲线是()A.两条射线B.两个半圆C.一个圆D.两个圆三、直线与圆位置关系设直线l:Ax+By+C=0,圆C:(x-a)2+(y-b)2=r2,圆心到直线的距离为:d=Aa+Bb+CA2+B2用途:判断圆和直线的位置关系(几何法)三、直线与圆位置关系代数法:联立直线与圆的方程组,通过消去y或x转化为一元二次方程所求得的判别式∆来判断圆与直线的关系。检验下听课效果4.直线4x-3y+510=0与圆x2+y2+2x-6y-6=0的位置关系是()A.相交不过圆心B.相交过圆心C.相切D.相离检验下听课效果5.已知圆C与圆(x-1)2+y2=1关于直线y=-x对称,则圆的方程为()A.(x+1)2+y2=1B.x2+y2=1C.x2+(y+1)2=1D.x2+(y-1)2=1第三节圆锥曲线一二椭圆双曲线三抛物线四曲线与方程一、椭圆(一)定义1.定义Ⅰ:若F1,F2是两定点,P为动点,且𝑃𝐹1+𝑃𝐹2=2a>𝐹1𝐹2(a为常数)则P点的轨迹是椭圆。2.定义Ⅱ:若F1为定点,l为定直线,动点P到F1的距离与到定直线l的距离之比为常数e(0b>0)的离心率为e=32,则𝑏𝑎等于。考点1:椭圆方程及相关参数的问题检验下听课效果7.以椭圆𝑥225+𝑦216=1的右焦点为圆心,且与直线2x-y+4=0相切的圆的方程是()A.x2+y2-6x-11=0B.x2+y2+6x-11=0C.x2+y2-6x-29=0D.x2+y2+6x-29=0二、双曲线(一)定义定义Ⅰ:若F1,F2是两定点,𝑃𝐹1−𝑃𝐹2=2a<𝐹1𝐹2(a为常数),则动点P的轨迹是双曲线。定义...