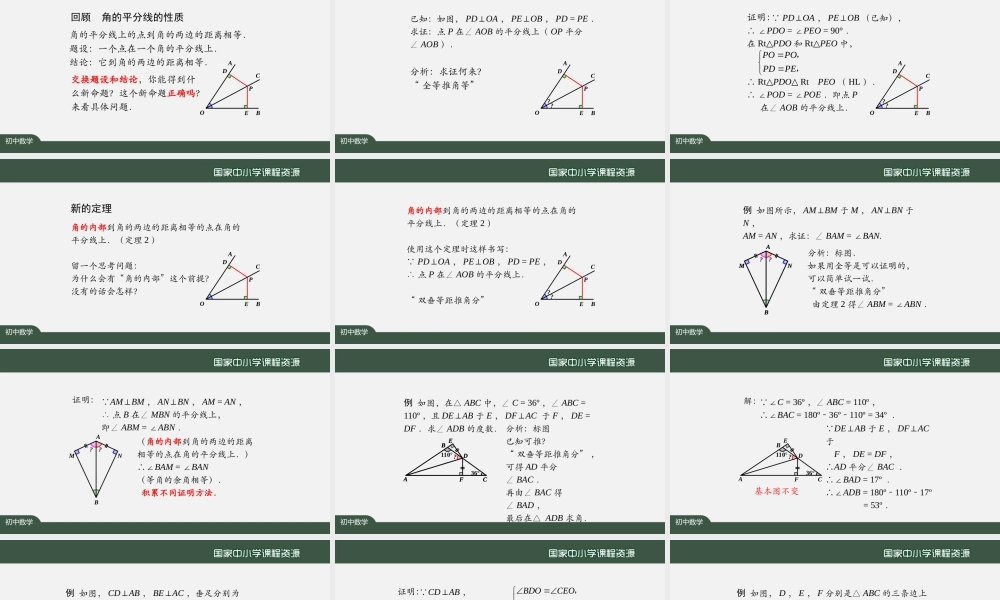
国家中小学课程资源角的平分线的性质(第三课时)年级:八年级学科:数学(人教版)主讲人:梁威学校:北京市第四中学初中数学回顾角的平分线的性质角的平分线上的点到角的两边的距离相等.题设:一个点在一个角的平分线上.结论:它到角的两边的距离相等.交换题设和结论,你能得到什么新命题?这个新命题正确吗?来看具体问题.EDAOBCP初中数学已知:如图,PD⊥OA,PE⊥OB,PD=PE.求证:点P在∠AOB的平分线上(OP平分∠AOB).分析:求证何来?“全等推角等”??EDAOBCP初中数学??EDAOBCP PD⊥OA,PE⊥OB(已知),∴∠PDO=∠PEO=90°.在Rt△PDO和Rt△PEO中,∴Rt△PDORt△△PEO(HL).∴∠POD=∠POE.即点P在∠AOB的平分线上.证明:POPOPDPE,,初中数学新的定理角的内部到角的两边的距离相等的点在角的平分线上.(定理2)留一个思考问题:为什么会有“角的内部”这个前提?没有的话会怎样?EDAOBCP初中数学角的内部到角的两边的距离相等的点在角的平分线上.(定理2)使用这个定理时这样书写: PD⊥OA,PE⊥OB,PD=PE,∴点P在∠AOB的平分线上.“双垂等距推角分”??EDAOBCP初中数学例如图所示,AM⊥BM于M,AN⊥BN于N,AM=AN,求证:∠BAM=∠BAN.分析:标图.如果用全等是可以证明的,可以简单试一试.“双垂等距推角分”由定理2得∠ABM=∠ABN.NBAM??NBAM初中数学 AM⊥BM,AN⊥BN,AM=AN,∴点B在∠MBN的平分线上,即∠ABM=∠ABN.(角的内部到角的两边的距离相等的点在角的平分线上.)∴∠BAM=∠BAN(等角的余角相等).积累不同证明方法.??NBAM证明:初中数学分析:标图已知可推?“双垂等距推角分”,可得AD平分∠BAC.再由∠BAC得∠BAD,最后在△ADB求角.例如图,在△ABC中,∠C=36º,∠ABC=110º,且DE⊥AB于E,DF⊥AC于F,DE=DF.求∠ADB的度数.FEDBAC110°36°?FEDBAC初中数学 ∠C=36º,∠ABC=110º,∴∠BAC=180º36º110º﹣﹣=34º. DE⊥AB于E,DF⊥AC于F,DE=DF,∴AD平分∠BAC.∴∠BAD=17º.∴∠ADB=180º110º17º﹣﹣=53º.解:110°36°?FEDBAC基本图不变初中数学例如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB=OC,连AO,求证:∠1=2∠.分析:标图已知可推?△ODB≌△OEC求证何来?全等?定理2更好需要OD=OE21ODEBAC21ODEBAC21ODEBAC初中数学 CD⊥AB,BE⊥AC,∴∠BDO=∠CEO=90°.在△ODB和△OEC中∴△ODB≌△OEC.∴OD=OE.又OD⊥AB,OE⊥AC,∴点O在∠BOC的平分线上,即∠1...