0521 -根号2有多大？-2PPT.pptxVIP免费

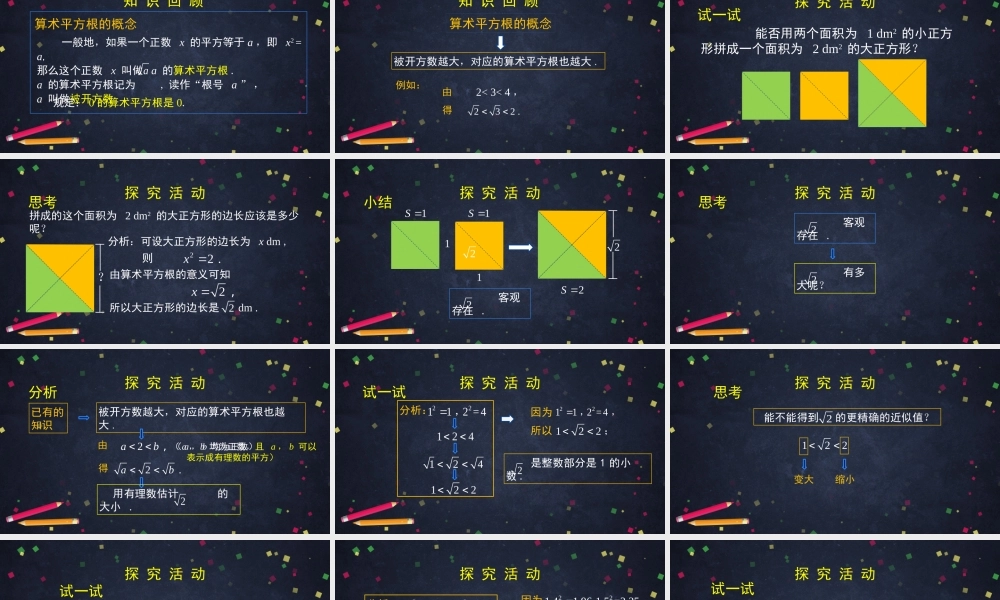
初一年级数学根号2有多大？主讲人刘青岩北京教育学院丰台分院知识回顾一般地，如果一个正数x的平方等于a，即x2=a,那么这个正数x叫做a的算术平方根.a的算术平方根记为,读作“根号a”，a叫做被开方数.a规定：0的算术平方根是0.算术平方根的概念知识回顾算术平方根的概念被开方数越大，对应的算术平方根也越大.232.由得2<3<4，例如：探究活动能否用两个面积为1dm2的小正方形拼成一个面积为2dm2的大正方形？试一试探究活动拼成的这个面积为2dm2的大正方形的边长应该是多少呢？思考22.x2x,分析：可设大正方形的边长为xdm,则由算术平方根的意义可知所以大正方形的边长是dm.2？探究活动小结客观存在.222112S1S1S探究活动思考客观存在.2有多大呢？22ab,由探究活动分析被开方数越大，对应的算术平方根也越大.已有的知识得2.ab用有理数估计的大小.2（a，b均为正数，且a，b可以表示成有理数的平方）（a，b均为正数）探究活动22112=4，124122分析：是整数部分是1的小数.2122因为所以；12422112=4，，试一试探究活动思考122变大缩小能不能得到的更精确的近似值？2探究活动试一试x1.11.21.31.41.51.61.71.81.9x21.211.441.691.962.252.562.893.243.611.9622.25.1.421.5.探究活动因为1.421.5;所以221.41.961.5=2.25，，21.41.9622.25分析：221.41.961.5=2.25，1.9622.251.421.5探究活动试一试x1.411.421.431.441.451.461.471.481.49x21.988122.0164.1.4121.42.1.452.10251.422.01641.9881探究活动1.4121.42;所以因为221.411.98811.42=2.0164，，分析：221.411.98811.42=2.0164，1.988122.01641.4121.421.988122.016421.41探究活动1.41421.415;因为所以221.414=1.9993961.415=2.002225，，能不能进一步精确的大小？2如此进行下去，可以得到的更精确的近似值．2小结2是无限不循环小数.2=1.414213562373∙∙∙2无限不循环小数是指小数位数无限，且小数部分不循环的小数．探究活动你能用刚才的方法估计的近似值吗?练一练3132，因为所以；22112=4，1.731.8，因为所以；221.7=2.891.8=3.24，是无限不循环小数.3=1.732050807568∙∙∙3小结2=1.414213562373∙∙∙许多正有理数的算术平方根(如：也是无限不循环小数.357,,）用计算器求出一个正有理数的算术平方根（或其近似值)．做一做大多数计算器...