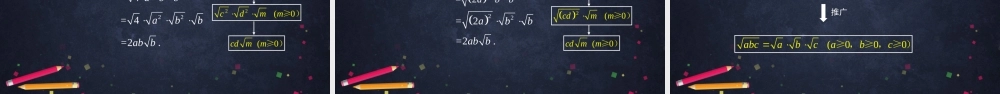0427 二次根式的乘法-2PPT.pptxVIP免费

初二年级数学二次根式的乘法主讲人刘璟北京汇文中学复习1.二次根式的定义:形如（a≥0）的式子.a2.二次根式的性质:（1）双重非负性:00aaa≥，且≥；（2）（3）2()(0)aaa≥；2(0).(0)aaaaaa≥＜35一个面积是3的正方形,它的边长是,一个面积是5的正方形,它的边长是;53一个面积是3的正方形,它的边长是,一个面积是5的正方形,它的边长是;若以这两个正方形的边去构造一个长方形,则它的面积是多少？535353=35S二次根式的乘法计算下列各式,并观察,你能发现什么规律？（1）,;（2）,;（3）,.49=49=1625=1625=254=254=计算下列各式,并观察计算结果,你能发现什么规律？（1）,;（2）,;（3）,.49=49=1625=1625=254=254=6620201010计算下列各式,并观察计算过程,你能发现什么规律？（1）,;（2）,;（3）,.49=49=1625=1625=254=254=23222345522=23=232(0aaa≥）22245=45=4522252=52=52你能再举几个例子验证一下吗？(00ababab≥，≥）一般地，二次根式的乘法法则是:(00aababb≥，≥）例1.计算:（1）35；（2）127.3例1.计算:=3535=15；(0abab≥）(00abab≥，≥）1.二次根式的乘法法则（1）解:2.有理数乘法915163154.＜＜，＜＜1=273=9=3.解:1.二次根式的乘法法则2.分数的乘法法则3.算术平方根的意义例1.计算:1273（2）1(0acca≥）(0abab≥）(00abab≥，≥）(0cc≥）例1.计算:（1）351273=35=15；1=273=9=3.（2）解：逆反(00ababab≥，≥）(00ababab≥，≥）积的算术平方根性质(00ababab≥，≥）例2.化简:（1）（2）234.ab1681；例2.化简:解1:=12961681=？解2:22=4916812=49=49=36；（1）1681；例2.化简:解3:=1681=49=36；1681（1）22cd(0abab≥）(00abab≥，≥）2.积的算术平方根性质3.算术平方根的意义cd1.完全平方数例2.化简:（2）234ab解:22cd(0abab≥）(00abab≥，≥）cd例2.化简:（2）234ab22=4abb=2.abb22=4abb解1:22(0cdmm≥）(0abab≥）(0cdmm≥）22(0cdmm≥）例2.化简:（2）234ab22=2abb=2.abb22=2abb2(0cdmm≥）(0abab≥）(0cdmm≥）2(0cdmm≥）解2:推广(00ababab≥，≥）积的算术平方根性质(000abcabcabc≥，≥，≥）例2.化简:（2）234ab22=2abb=2.abb22=2abb2(0cdmm≥）(0abab≥）(0cdm...