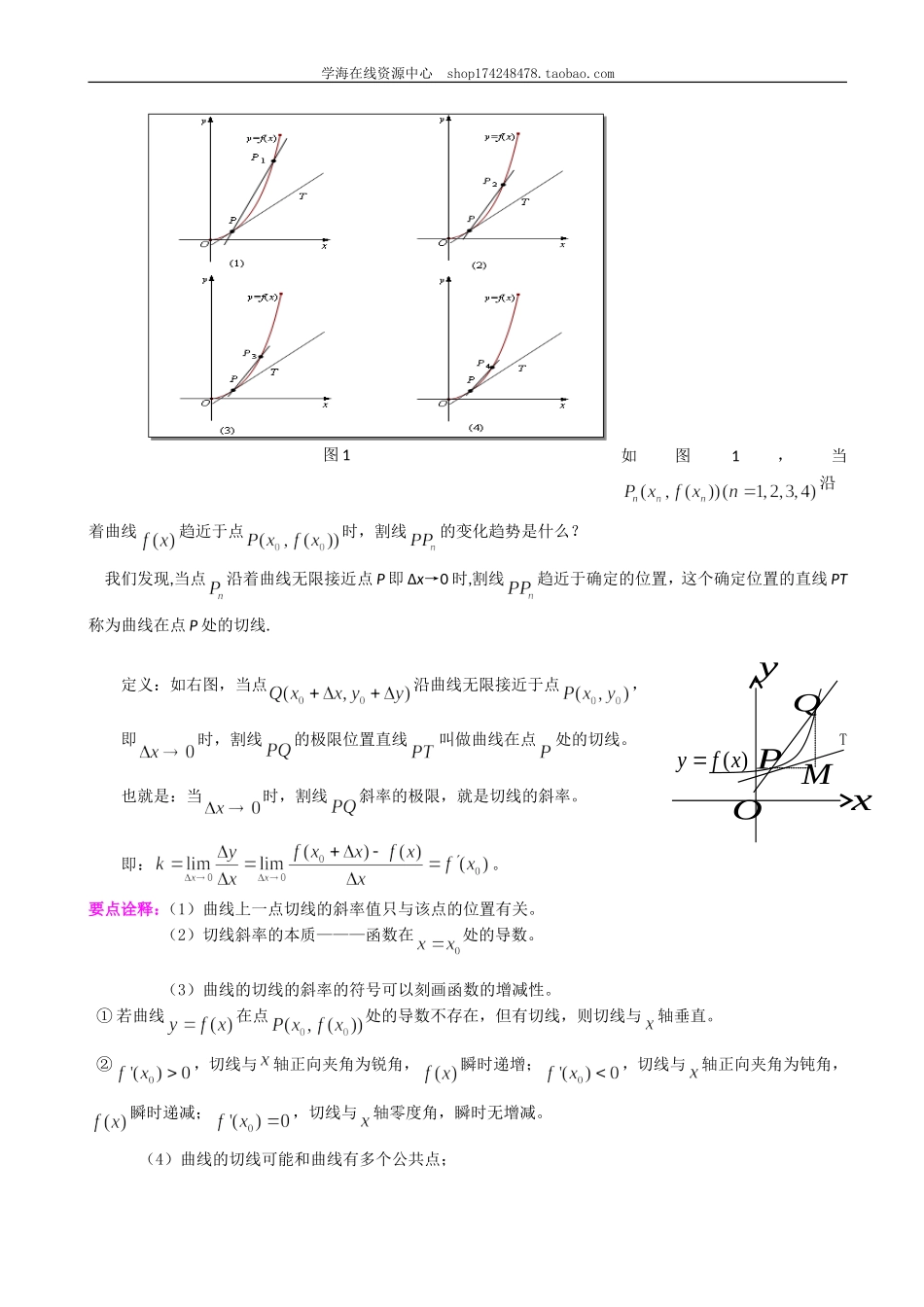
学海在线资源中心shop174248478.taobao.com导数的几何意义编稿:赵雷审稿:李霞【学习目标】1.理解导数的几何意义。2.理解导数的全面涵义。3.掌握利用导数求函数图象的切线的斜率。4.会求过点(或在点处)的切线方程。【要点梳理】(根据课标要求进行适当的深化与拓展。)要点一、导数几何意义1.平均变化率的几何意义——曲线的割线函数的平均变化率的几何意义是表示连接函数图像上两点割线的斜率。如图所示,函数的平均变化率的几何意义是:直线AB的斜率。事实上,。换一种表述:曲线上一点及其附近一点,经过点、作曲线的割线,则有。要点诠释:根据平均变化率的几何意义,可求解有关曲线割线的斜率。2.导数的几何意义——曲线的切线xyO()yfxQPM学海在线资源中心shop174248478.taobao.com如图1,当沿着曲线趋近于点时,割线的变化趋势是什么?我们发现,当点沿着曲线无限接近点P即Δx→0时,割线趋近于确定的位置,这个确定位置的直线PT称为曲线在点P处的切线.定义:如右图,当点沿曲线无限接近于点,即时,割线的极限位置直线叫做曲线在点处的切线。T也就是:当时,割线斜率的极限,就是切线的斜率。即:。要点诠释:(1)曲线上一点切线的斜率值只与该点的位置有关。(2)切线斜率的本质———函数在处的导数。(3)曲线的切线的斜率的符号可以刻画函数的增减性。①若曲线在点处的导数不存在,但有切线,则切线与轴垂直。②,切线与轴正向夹角为锐角,瞬时递增;,切线与轴正向夹角为钝角,瞬时递减;,切线与轴零度角,瞬时无增减。(4)曲线的切线可能和曲线有多个公共点;xyO()yfxQPM图1学海在线资源中心shop174248478.taobao.com为什么要用割线的极限位置来定义切线,而不说“与曲线只有一个公共点的直线叫做切线?”过去我们定义圆的切线就是“与圆有且只有一个公共点的直线”,这个定义符合圆、椭圆等一类曲线,那么,能否对任何曲线C都用“与C有且只有一个公共点”来定义C的切线呢?如图1-1-2-1的曲线C是我们熟知的正弦曲线y=sinx的一部分,直线2显然与曲线C有唯一公共点M,但我们不能说直线2与曲线C相切;而直线1尽管与曲线C有不止一个公共点,但我们可以说直线1是曲线C在点N处的切线。要点二、曲线的切线(1)用导数的几何意义求曲线的切线方程的方法步骤:①求出切点的坐标;②求出函数在点处的导数③得切线方程(2)在点处的切线与过点(x0,y0)的切线的区别。在点处的切线是说明点为此切线的切点;而过点(x0,y0)的切线...