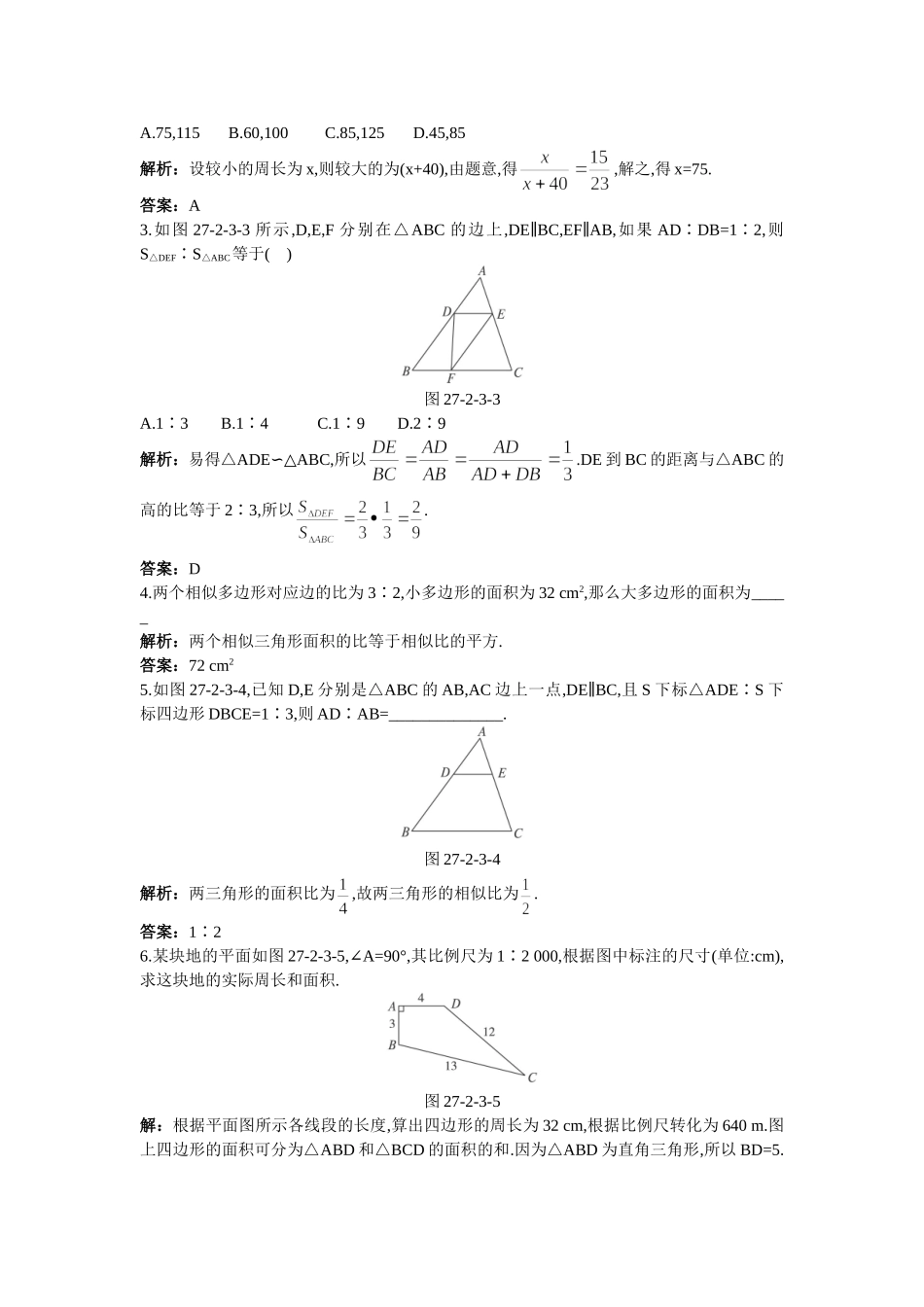
27.2.3相似三角形的周长与面积5分钟训练(预习类训练,可用于课前)1.若,则=_____________.解析:由题意,得b=2a,d=2c,f=2e,代入化简可得答案.答案:2.如图27-2-3-1,D,E分别是△ABC中AB,AC边上的中点,则SADE△S∶ABC△=________________.图27-2-3-1解析:两三角形的相似比为,故面积比为.答案:14∶3.如图27-2-3-2,D,E分别是△ABC的边AB,AC上的点,且DEBC,BE∥交DC于F点,EFFB=13,∶∶则SADE△S∶ABC△的值为()图27-2-3-2A.13B.19∶∶C.1∶D.以上答案都不对解析:由△DEFCBF∽△求得DE与BC的比,再由△ADEABC∽△求得面积的比.答案:B4.在一张由复印机复印出来的纸上,一个多边形的一条边的长由原来的1cm变成4cm,那么它的周长由原来的3cm变成()A.6cmB.12cmC.24cmD.48cm解析:复印图形相似,相似比等于周长比,故变成12cm.答案:B10分钟训练(强化类训练,可用于课中)1.将一个五边形改成与它相似的五边形,如果面积扩大为原来的9倍,那么周长扩大为原来的()A.9倍B.3倍C.81倍D.18倍解析:根据相似三角形的周长与面积的关系求解.答案:B2.两个相似三角形的一组对应边的长分别是15和23,它们周长的差是40,则这两个三角形的周长分别为()[来源:学。科。网Z。X。X。K]A.75,115B.60,100C.85,125D.45,85解析:设较小的周长为x,则较大的为(x+40),由题意,得,解之,得x=75.答案:A3.如图27-2-3-3所示,D,E,F分别在△ABC的边上,DEBC,EFAB,∥∥如果ADDB=12,∶∶则SDEF△S∶ABC△等于()图27-2-3-3A.13B.14C.19D.29∶∶∶∶解析:易得△ADEABC,∽△所以.DE到BC的距离与△ABC的高的比等于23,∶所以.答案:D4.两个相似多边形对应边的比为32,∶小多边形的面积为32cm2,那么大多边形的面积为_____解析:两个相似三角形面积的比等于相似比的平方.答案:72cm25.如图27-2-3-4,已知D,E分别是△ABC的AB,AC边上一点,DEBC,∥且S下标△ADES∶下标四边形DBCE=13,∶则ADAB=______________.∶图27-2-3-4解析:两三角形的面积比为,故两三角形的相似比为.答案:12∶6.某块地的平面如图27-2-3-5,A=90°,∠其比例尺为12000,∶根据图中标注的尺寸(单位:cm),求这块地的实际周长和面积.图27-2-3-5解:根据平面图所示各线段的长度,算出四边形的周长为32cm,根据比例尺转化为640m.图上四边形的面积可分为△ABD和△BCD的面积的和.因为△ABD为直角三角形,所以BD=5.又CD=12,BC=13,所以△BCD为直角三角形,四边形的面积为×3×4+×12×5=36.利用比例尺折合为14400m2.30分钟训练(巩固类训练,可用于课后)1.如图27-2-3...