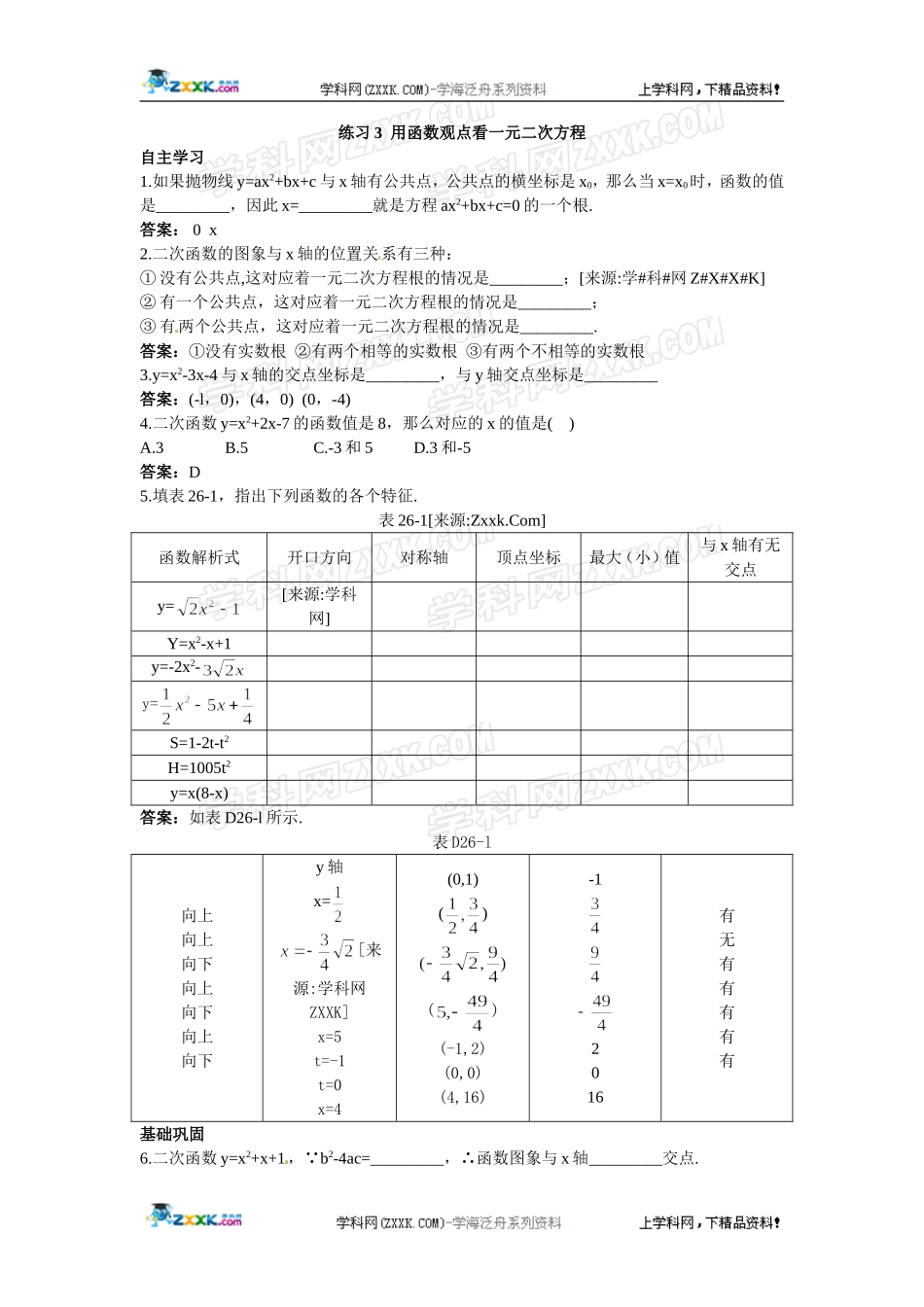
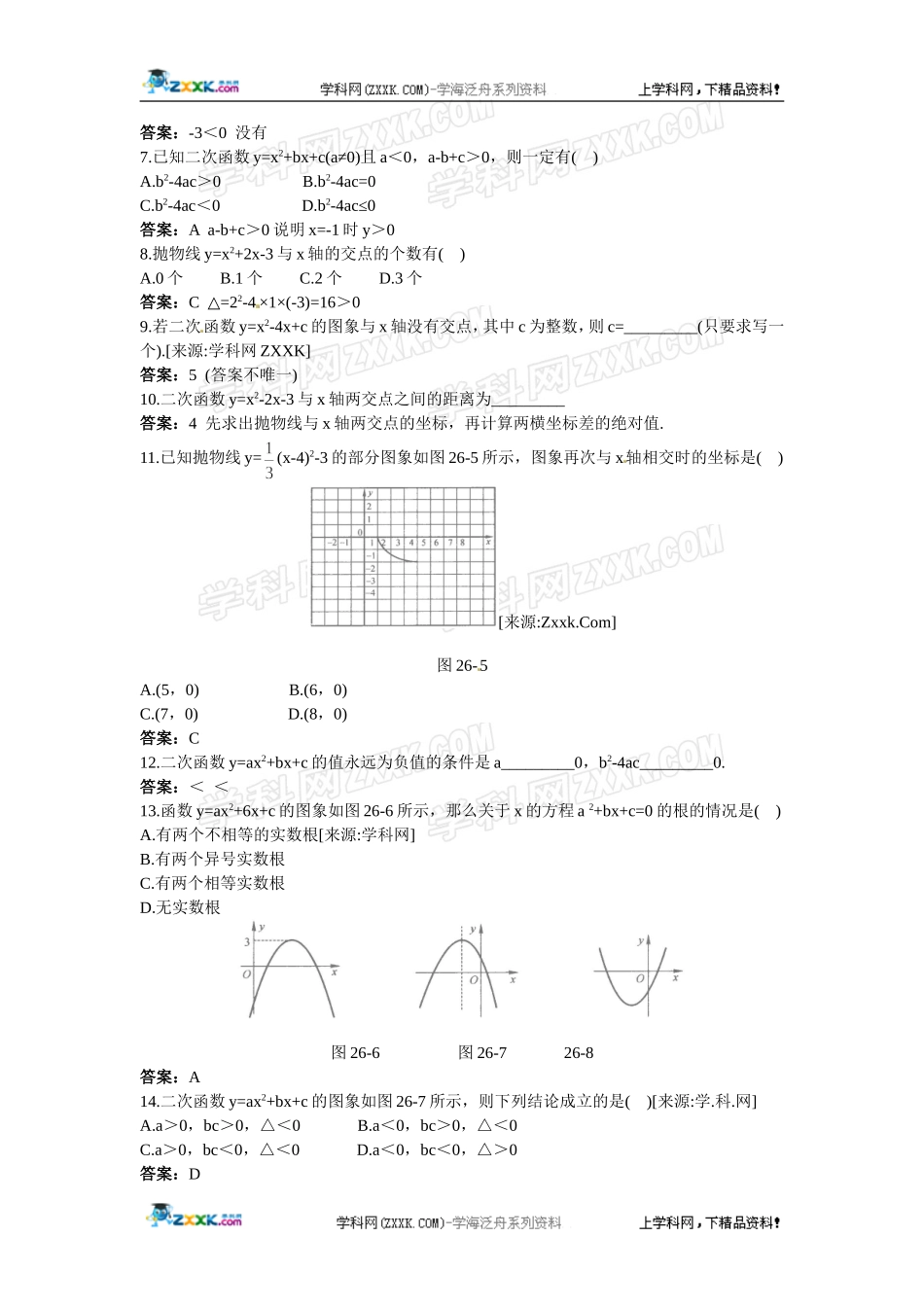
练习3用函数观点看一元二次方程自主学习1.如果抛物线y=ax2+bx+c与x轴有公共点,公共点的横坐标是x0,那么当x=x0时,函数的值是_________,因此x=_________就是方程ax2+bx+c=0的一个根.答案:0x2.二次函数的图象与x轴的位置关系有三种:①没有公共点,这对应着一元二次方程根的情况是_________;[来源:学#科#网Z#X#X#K]②有一个公共点,这对应着一元二次方程根的情况是_________;③有两个公共点,这对应着一元二次方程根的情况是_________.答案:①没有实数根②有两个相等的实数根③有两个不相等的实数根3.y=x2-3x-4与x轴的交点坐标是_________,与y轴交点坐标是_________答案:(-l,0),(4,0)(0,-4)4.二次函数y=x2+2x-7的函数值是8,那么对应的x的值是()A.3B.5C.-3和5D.3和-5答案:D5.填表26-1,指出下列函数的各个特征.表26-1[来源:Zxxk.Com]函数解析式开口方向对称轴顶点坐标最大(小)值与x轴有无交点y=[来源:学科网]Y=x2-x+1y=-2x2-y=S=1-2t-t2H=1005t2y=x(8-x)答案:如表D26-l所示.表D26-l向上向上向下向上向下向上向下y轴x=[来源:学科网ZXXK]x=5t=-1t=0x=4(0,1)()()(-1,2)(0,0)(4,16)-12016有无有有有有有基础巩固6.二次函数y=x2+x+1, b2-4ac=_________,∴函数图象与x轴_________交点.答案:-3<0没有7.已知二次函数y=x2+bx+c(a≠0)且a<0,a-b+c>0,则一定有()A.b2-4ac>0B.b2-4ac=0C.b2-4ac<0D.b2-4ac≤0答案:Aa-b+c>0说明x=-1时y>08.抛物线y=x2+2x-3与x轴的交点的个数有()A.0个B.1个C.2个D.3个答案:C=2△2-4×1×(-3)=16>09.若二次函数y=x2-4x+c的图象与x轴没有交点,其中c为整数,则c=_________(只要求写一个).[来源:学科网ZXXK]答案:5(答案不唯一)10.二次函数y=x2-2x-3与x轴两交点之间的距离为_________答案:4先求出抛物线与x轴两交点的坐标,再计算两横坐标差的绝对值.11.已知抛物线y=(x-4)2-3的部分图象如图26-5所示,图象再次与x轴相交时的坐标是()[来源:Zxxk.Com]图26-5A.(5,0)B.(6,0)C.(7,0)D.(8,0)答案:C12.二次函数y=ax2+bx+c的值永远为负值的条件是a_________0,b2-4ac_________0.答案:<<13.函数y=ax2+6x+c的图象如图26-6所示,那么关于x的方程a2+bx+c=0的根的情况是()A.有两个不相等的实数根[来源:学科网]B.有两个异号实数根C.有两个相等实数根D.无实数根图26-6图26-726-8答案:A14.二次函数y=ax2+bx+c的图象如图26-7所示,则下列结论成立的是()[来源:学.科.网]A.a>0,bc>0,△<0B.a<0,bc>0,△<...