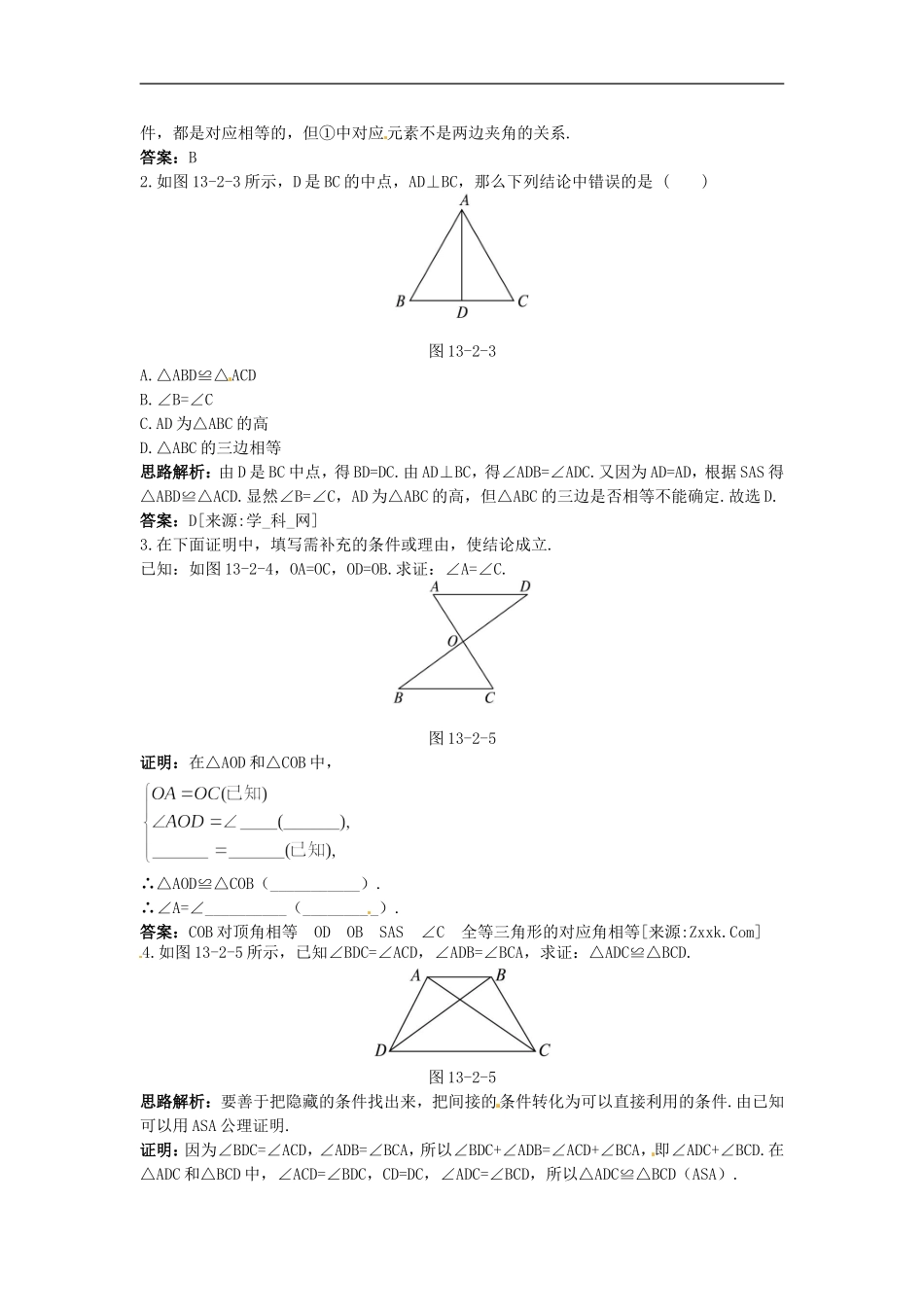
13.2三角形全等的条件(一)5分钟训练(预习类训练,可用于课前)1.图13-2-1中两个三角形的关系是()[来源:学.科.网]图13-2-1A.不全等B.它们的周长不相等C.全等D.不确定思路解析:根据三角形内角和等于180°,得180°-140°-20°=20°,两三角形有一条公共边,根据ASA可得两个三角形全等.答案:C2.在△ABC和△A1B1C1中,已知AB=A1B1,∠A=∠A1,若要证△ABC≌△A1B1C1,还需要()A.∠B=∠B1B.∠C=∠C1C.AC=A1C1D.以上全对思路解析:选择A项条件,根据ASA可以证明△ABC和△A1B1C1全等;选择B项条件,根据AAS可以证明△ABC和△A1B1C1全等;选择C项条件,根据SAS可以证明△ABC和△A1B1C1全等.故应选D.答案:D3.如图13-2-2,点A、C、B、D在同一直线上,AM=CN,BM=DN,AC=DB.图13-2-2问:AM与CN有怎样的位置关系?解:AM∥CN.理由: AC=BD,∴AB=CD().在△ABM与△CDN中,∴△ABM≌△CDN().∴∠A=∠1().∴AM∥CN().思路解析:填写推理理由,第一个推理中用到了AC-BC=BD-BC,是等式性质的运用.答案:等式的性质SSS全等三角形对应角相等同位角相等,两直线平行10分钟训练(强化类训练,可用于课中)1.下面条件:①AB=DE,∠A=∠D,BC=EF;②BC=EF,AC=DF,∠C=∠F,③AB=DE,BC=EF,AC=DF.能判断△ABC≌△DEF的是()A.①②B.②③C.①③D.①②③思路解析:题目给定了三角形全等的表达式,由此就确定了边角的对应关系,观察这三组条件,都是对应相等的,但①中对应元素不是两边夹角的关系.答案:B2.如图13-2-3所示,D是BC的中点,AD⊥BC,那么下列结论中错误的是()图13-2-3A.△ABD≌△ACDB.∠B=∠CC.AD为△ABC的高D.△ABC的三边相等思路解析:由D是BC中点,得BD=DC.由AD⊥BC,得∠ADB=∠ADC.又因为AD=AD,根据SAS得△ABD≌△ACD.显然∠B=∠C,AD为△ABC的高,但△ABC的三边是否相等不能确定.故选D.答案:D[来源:学_科_网]3.在下面证明中,填写需补充的条件或理由,使结论成立.已知:如图13-2-4,OA=OC,OD=OB.求证:∠A=∠C.图13-2-5证明:在△AOD和△COB中,∴△AOD≌△COB(___________).∴∠A=∠__________(_________).答案:COB对顶角相等ODOBSAS∠C全等三角形的对应角相等[来源:Zxxk.Com]4.如图13-2-5所示,已知∠BDC=∠ACD,∠ADB=∠BCA,求证:△ADC≌△BCD.图13-2-5思路解析:要善于把隐藏的条件找出来,把间接的条件转化为可以直接利用的条件.由已知可以用ASA公理证明.证明:因为∠BDC=∠ACD,∠ADB=∠BCA,所以∠BDC+∠ADB=∠ACD+∠B...