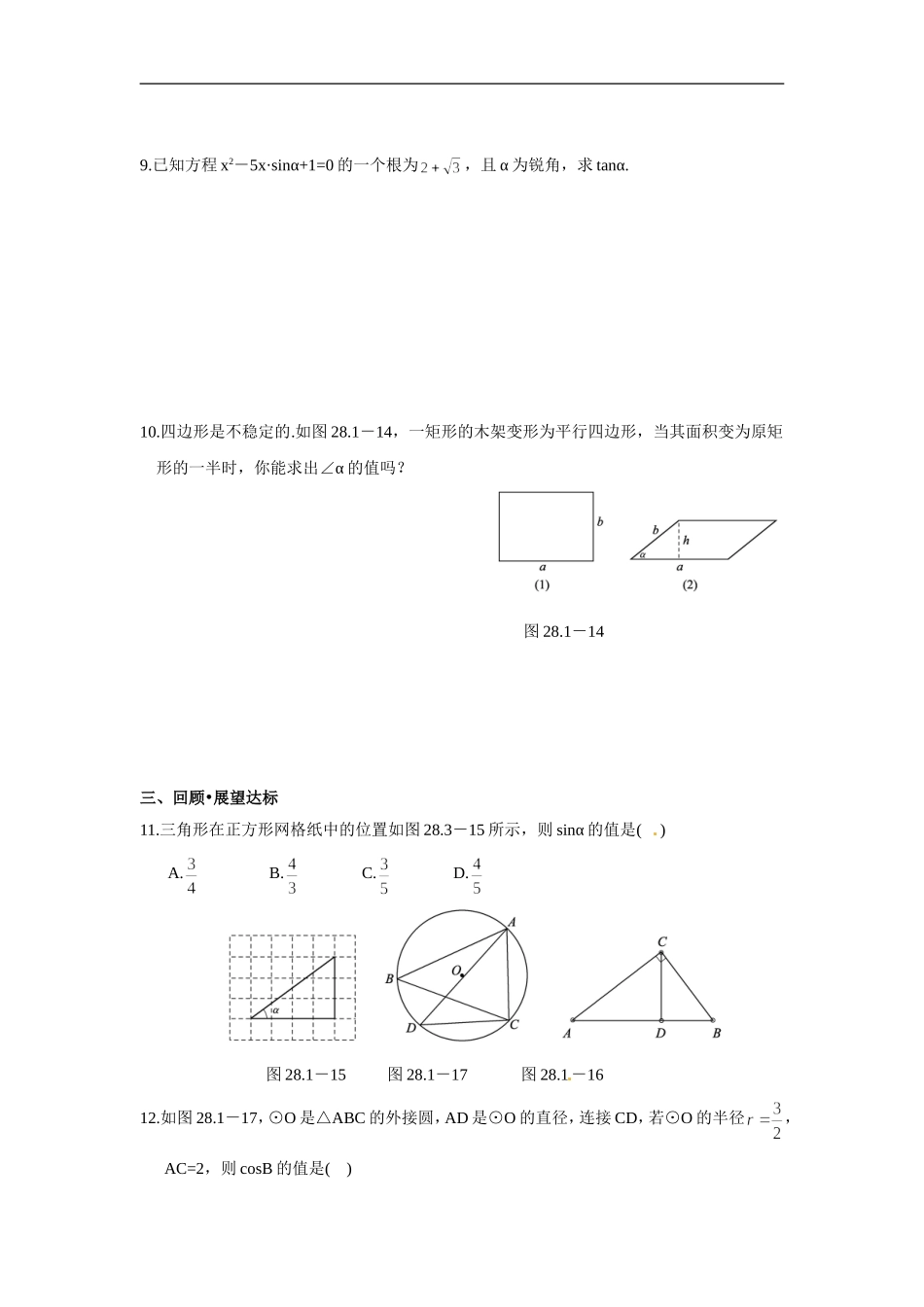
28.1锐角三角函数——正弦、余弦、正切一、基础·巩固达标1.在RtABC△中,如果各边长度都扩大2倍,则锐角A的正弦值和余弦值()A.都没有变化B.都扩大2倍C.都缩小2倍D.不能确定2.已知α是锐角,且cosα=,则sinα=()A.B.C.D.3.RtABC△中,∠C=90°,ACBC=1∶∶,则cosA=_______,tanA=_________.4.设α、β为锐角,若sinα=,则α=________;若tanβ=,则β=_________.5.用计算器计算:sin51°30′+cos49°50′-tan46°10′的值是_________.6.ABC△中,∠BAC=90°,AD是高,BD=9,tanB=,求AD、AC、BC.二、综合•应用达标7.已知α是锐角,且sinα=,则cos(90°-α)=()A.B.C.D.8.若α为锐角,tana=3,求的值.9.已知方程x2-5x·sinα+1=0的一个根为,且α为锐角,求tanα.10.四边形是不稳定的.如图28.1-14,一矩形的木架变形为平行四边形,当其面积变为原矩形的一半时,你能求出∠α的值吗?图28.1-14三、回顾•展望达标11.三角形在正方形网格纸中的位置如图28.3-15所示,则sinα的值是()A.B.C.D.图28.1-15图28.1-17图28.1-1612.如图28.1-17,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径,AC=2,则cosB的值是()A.B.C.D.13.在△ABC中,∠C=90°,AB=15,sinA=,则BC=()A.45B.5C.D.14.如图28.3-16,CD是RtABC△斜边上的高,AC=4,BC=3,则cosBCD=()∠A.B.C.D.15.课本中,是这样引入“锐角三角函数”的:如图28.1-18,在锐角α的终边OB上,任意取两点P和P1,分别过点P和P1做始边OA的垂线PM和P1M1,M和M1为垂足.我们规定,比值________叫做角α的正弦,比值________叫做角α的余弦.这是因为,由相似三角形的性质,可推得关于这些比值得两个等式:________,________.说明这些比值都是由________唯一确定的,而与P点在角的终边上的位置无关,所以,这些比值都是自变量α的函数.图28.1-18图28.1-1916.计算:2-1-tan60°+(-1)0+;17.已知:如图28.1-19,△ABC内接于⊙O,点D在OC的延长线上,sinB=,∠CAD=30°.(1)求证:AD是⊙O的切线;(2)若ODAB⊥,BC=5,求AD的长.[来源:Z#xx#k.Com]参考答案一、基础·巩固达标1.在RtABC△中,如果各边长度都扩大2倍,则锐角A的正弦值和余弦值()A.都没有变化B.都扩大2倍C.都缩小2倍D.不能确定思路解析:当RtABC△的各边长度都扩大二倍,所得新三角形与原三角形相似,故锐角A大小不变.答案:A2.已知α是锐角,且cosα=,则sinα=()A.B.C.D.思路解析:由cosα=,可以设α的邻边为4k,斜边为5k,...