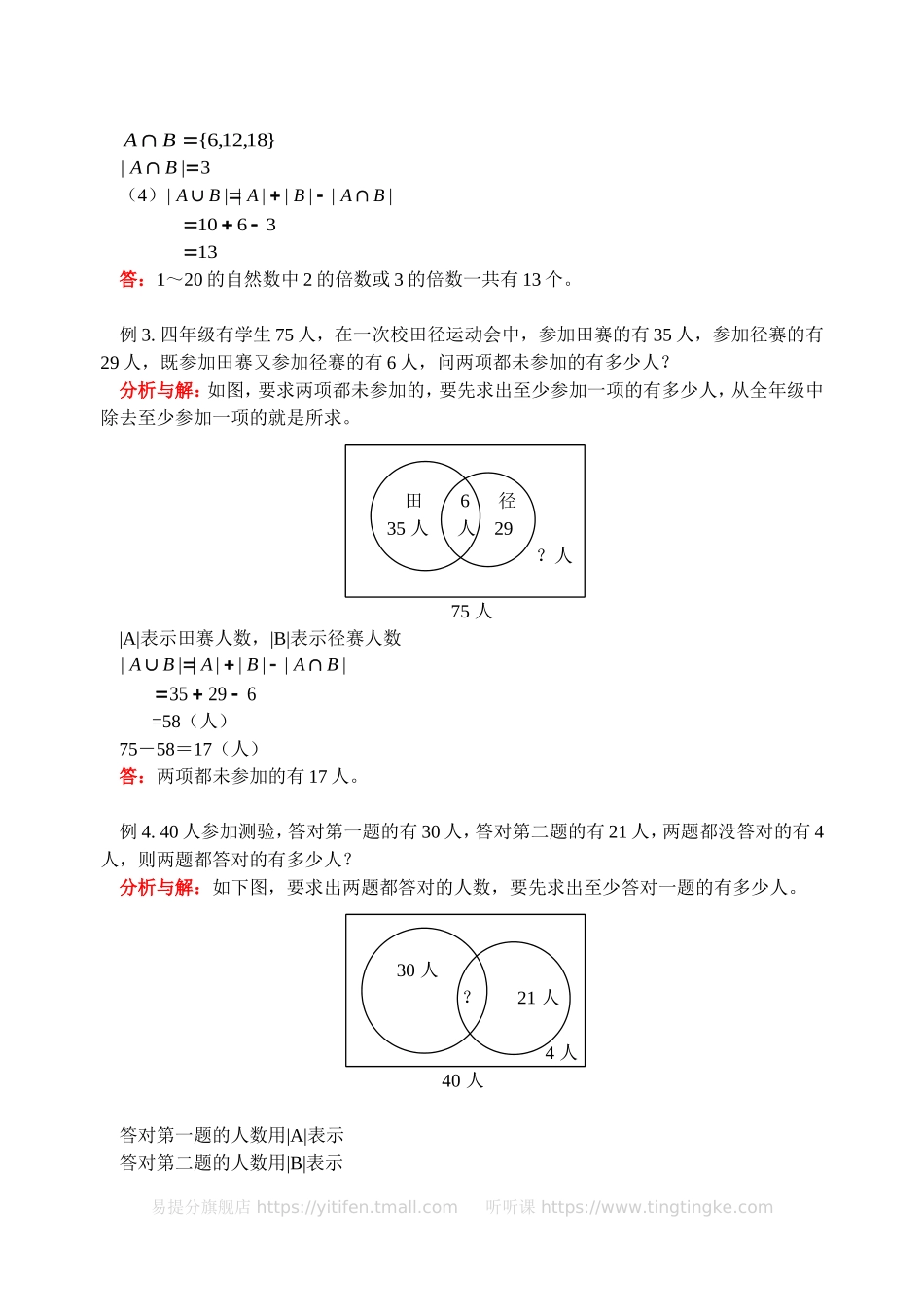
包含与排除(二)在日常生活中,我们需要把具有相同性质的对象放在一起考虑,并且给它一个总称。如钢笔、铅笔、本、橡皮……总称为文具;西红柿、黄瓜、土豆、白菜……总称为蔬菜;苹果、香蕉、梨……总称为水果等等。在数学里,我们把具有某种相同性质的对象放在一起考虑,这些相同性质的对象便组成了一个“集合”,每个集合总是由一些成员组成的,集合中的这些成员叫做这个集合的元素。名词解释:(1)由所有属于集合A或属于集合B的元素所组成的集合,叫做集合A、B的并集(又叫A与B的和)。记作BA,记号“”读作“并”,BA读作“A并B”。(2)A、B两个集合公共的元素,也就是那些既属于A,又属于B的元素,它们所组成的集合叫做A和B的交集,记作“BA”,记号“”读作“交”,BA读作“A交B”。下面我们就利用“集合”的知识来解决有关“包含与排除”问题。(一)典型例题例1.六一班同学参加数学小组和作文小组,其中参加数学小组的有16人,参加作文小组的有20人,两组都参加的有5人,六一班参加数学小组或作文小组的一共有多少人?分析与解:参加数学小组的可以看成集合|A|,参加作文小组的可以看成是集合|B|,两组都参加的可以看成||BA,问题是求参加数学小组或作文小组的一共有多少人,也就是把集合|A|和集合|B|合并在一起,即||BA3152016(人)根据上面列式,我们可以得出:||||||||BABABA答:参加数学小组或作文小组的一共有31人。例2.求1~20的自然数中2的倍数或3的倍数的个数。分析与解:(1)1~20的自然数中2的倍数用集合A表示A={2,4,6,8,10,12,14,16,18,20}|A|=10(2)1~20的自然数中3的倍数用集合B表示B={3,6,9,12,15,18}|B|=6(3)既是2的倍数又是3的倍数,也就是BA易提分旗舰店https://yitifen.tmall.com听听课https://www.tingtingke.com}18,12,6{BA3||BA(4)||||||||BABABA133610答:1~20的自然数中2的倍数或3的倍数一共有13个。例3.四年级有学生75人,在一次校田径运动会中,参加田赛的有35人,参加径赛的有29人,既参加田赛又参加径赛的有6人,问两项都未参加的有多少人?分析与解:如图,要求两项都未参加的,要先求出至少参加一项的有多少人,从全年级中除去至少参加一项的就是所求。田6径35人人29?人75人|A|表示田赛人数,|B|表示径赛人数||||||||BABABA62935=58(人)75-58=17(人)答:两项都未参加的有17人。例4.40人参加...