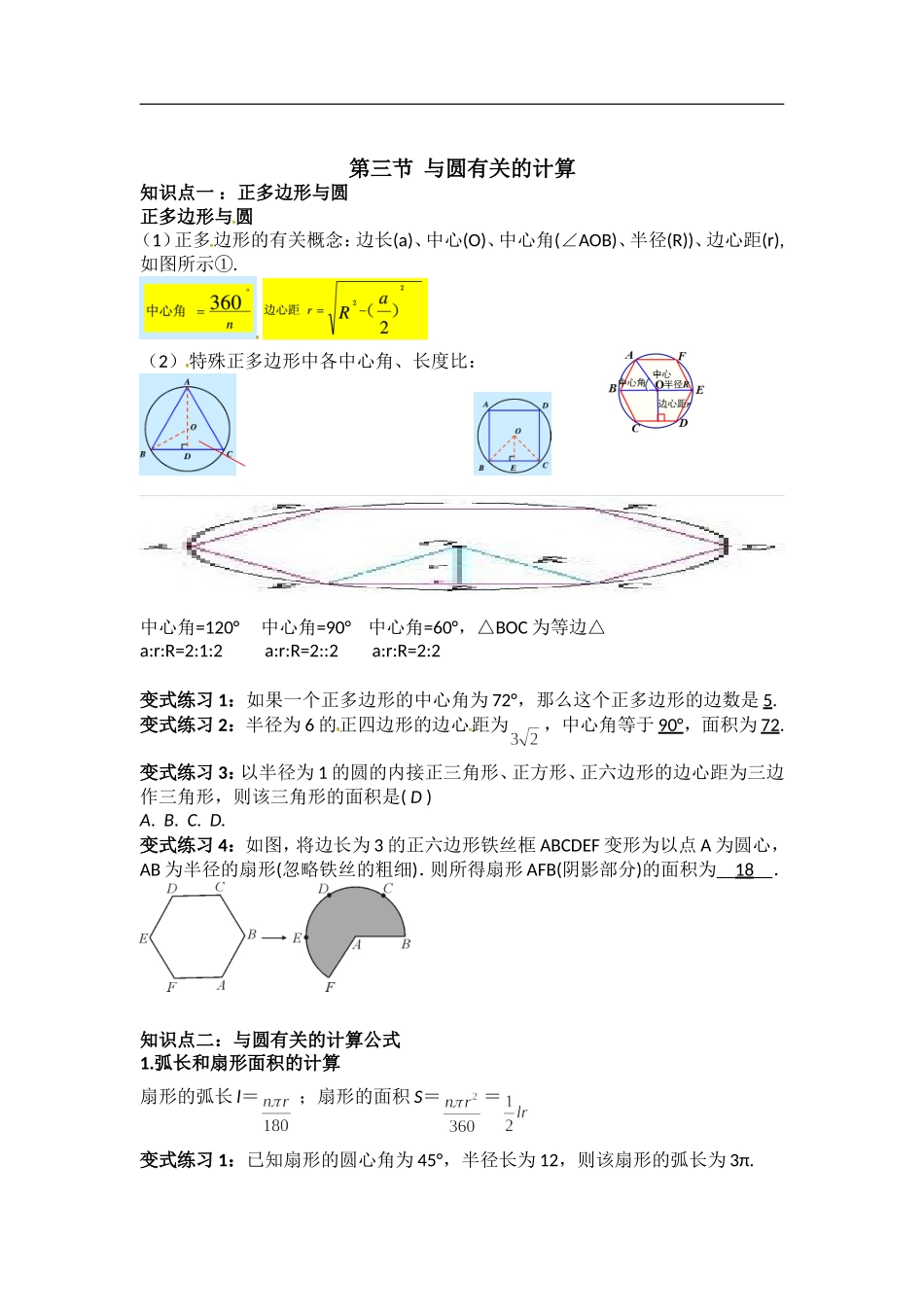
第三节与圆有关的计算知识点一:正多边形与圆正多边形与圆(1)正多边形的有关概念:边长(a)、中心(O)、中心角(∠AOB)、半径(R))、边心距(r),如图所示①.(2)特殊正多边形中各中心角、长度比:中心角=120°中心角=90°中心角=60°,△BOC为等边△a:r:R=2:1:2a:r:R=2::2a:r:R=2:2变式练习1:如果一个正多边形的中心角为72°,那么这个正多边形的边数是5.变式练习2:半径为6的正四边形的边心距为,中心角等于90°,面积为72.变式练习3:以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是(D)A.B.C.D.变式练习4:如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为__18__.知识点二:与圆有关的计算公式1.弧长和扇形面积的计算扇形的弧长l=;扇形的面积S==[来源变式练习1:已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为3π.变式练习2:如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形DAB的面积为()第2题图A.6B.7C.8D.9【解析】D根据扇形的面积公式进行计算,由题意可知l=3+3=6,∴S扇形DAB=lr=×6×3=9.2.圆锥与侧面展开图(1)圆锥侧面展开图是一个扇形,扇形的半径等于圆锥的母线,扇形的弧长等于圆锥的底面周长.(2)计算公式:,S侧==πrl变式练习1:如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中的长是________cm(计算结果保留π).第1题图【解析】10π由勾股定理得圆锥底面圆的半径r===5cm,则圆锥侧面展开扇形的弧长等于圆锥底面圆的周长:lAC=2πr=10πcm.变式练习2:如图,三个小正方形的边长都为1,则图中阴影部分面积的和是____注意:在求不规则图形的面积时,注意利用割补法与等积变化方法归为规则图形再利用规则图形的公式求解.____(结果保留π).第2题图【解析】π如解图, 在Rt△BDC中,∠DBC+∠BDC=90°,∠ABE=45°,∴三个圆心角之和为∠ABE+∠DBC+∠BDC=45°+90°=135°.三个扇形的半径为1,利用扇形面积公式S=得:S阴影==π.第2题解图变式练习3:如图,在ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是________(结果保留π).第3题图【解析】3-如解图,过点D作DF⊥AB,垂足为F, AD=2,∠A=30°...