三角形的分割（二）(含答案)-.docVIP免费

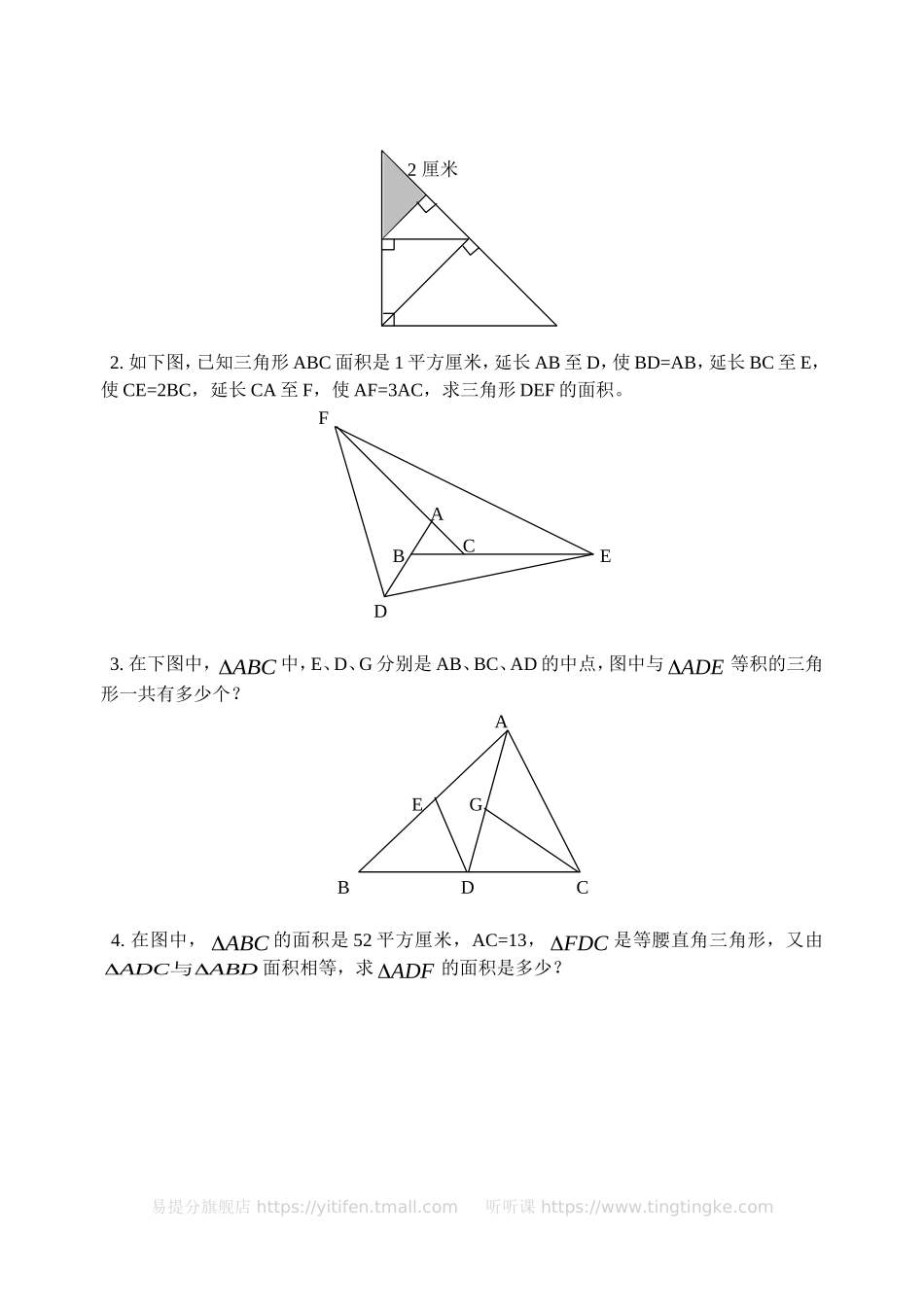
三角形的分割（二）同学们大家好！在上一讲中，我们一起研究了“三角形的分割”的一些知识。其中有一条很重要的知识“等底等高的三角形面积相等”。今天我们这一讲一起来研究这些知识的应用。【典型例题】一.阅读思考：例1.如图，点D、E、F与点G、H、N分别是三角形ABC与三角形DEF各边的中点。那么阴影部分的三角形面积的和是三角形ABC的面积的()()。（十一届迎春杯决赛题）ADGFHNBEC分析与解答：因为D、E、F分别为AB、BC、AC的中点，所以DE、EF、DF分别平行于AC、AB、BC，所以BDEEFC和是等底等高的三角形，EFCDE和，BDEDEF和分别是等底等高的三角形。解：SSDEFABC14SSSSSSSGHNDEFABCDEFGHNABC12116316阴即SSABC阴316例2.下图中，三角形ABC的面积是12平方厘米。并且BE=2EC，F是CD的中点。那么阴影部分的面积是（）平方厘米。（第十二届迎春杯训练题）易提分旗舰店https://yitifen.tmall.com听听课https://www.tingtingke.comCEADBF分析与解答：因为ACEABE和的高相等，而BE=2EC，所以ABE的面积是ACE面积的2倍。解：SABE8（平方厘米）SACE4（平方厘米）又因为SSSSACFADFBCFBDF,所以SSSACFBCFABC126（平方厘米）于是SSSSBEFACFBCFACE()642()平方厘米又SSCEFBEF122121（平方厘米）所以SSSSBDFBCFBEFCEF213（平方厘米）SSSBDFBEF阴影325（平方厘米）【模拟试题】（答题时间：30分钟）二.尝试练习：1.有一张等腰直角三角形的纸片，沿它的斜边上的高把这个三角形对折；再沿小三角形的斜边上的高把它对折；再沿更小三角形斜边上的高把它对折。这时，得到一个直角边的长是2厘米的等腰直角三角形（如下图中阴影部分）。那么，原来的等腰直角三角形纸片的面积是多少平方厘米？易提分旗舰店https://yitifen.tmall.com听听课https://www.tingtingke.com2厘米2.如下图，已知三角形ABC面积是1平方厘米，延长AB至D，使BD=AB，延长BC至E，使CE=2BC，延长CA至F，使AF=3AC，求三角形DEF的面积。FBEDAC3.在下图中，ABC中，E、D、G分别是AB、BC、AD的中点，图中与ADE等积的三角形一共有多少个？AEGBDC4.在图中，ABC的面积是52平方厘米，AC=13，FDC是等腰直角三角形，又由ADCABD与面积相等，求ADF的面积是多少？易提分旗舰店https://yitifen.tmall.com听听课https://www.tingtingke.comAFCDB5.A是所在边上的中点，B点在边上距顶点C三分之一处，阴影部分SABC5，那么SABD（），SACE（）DAEBC易提分旗舰店https://yitifen.tmall.com听听课https://www.tingtingke.com