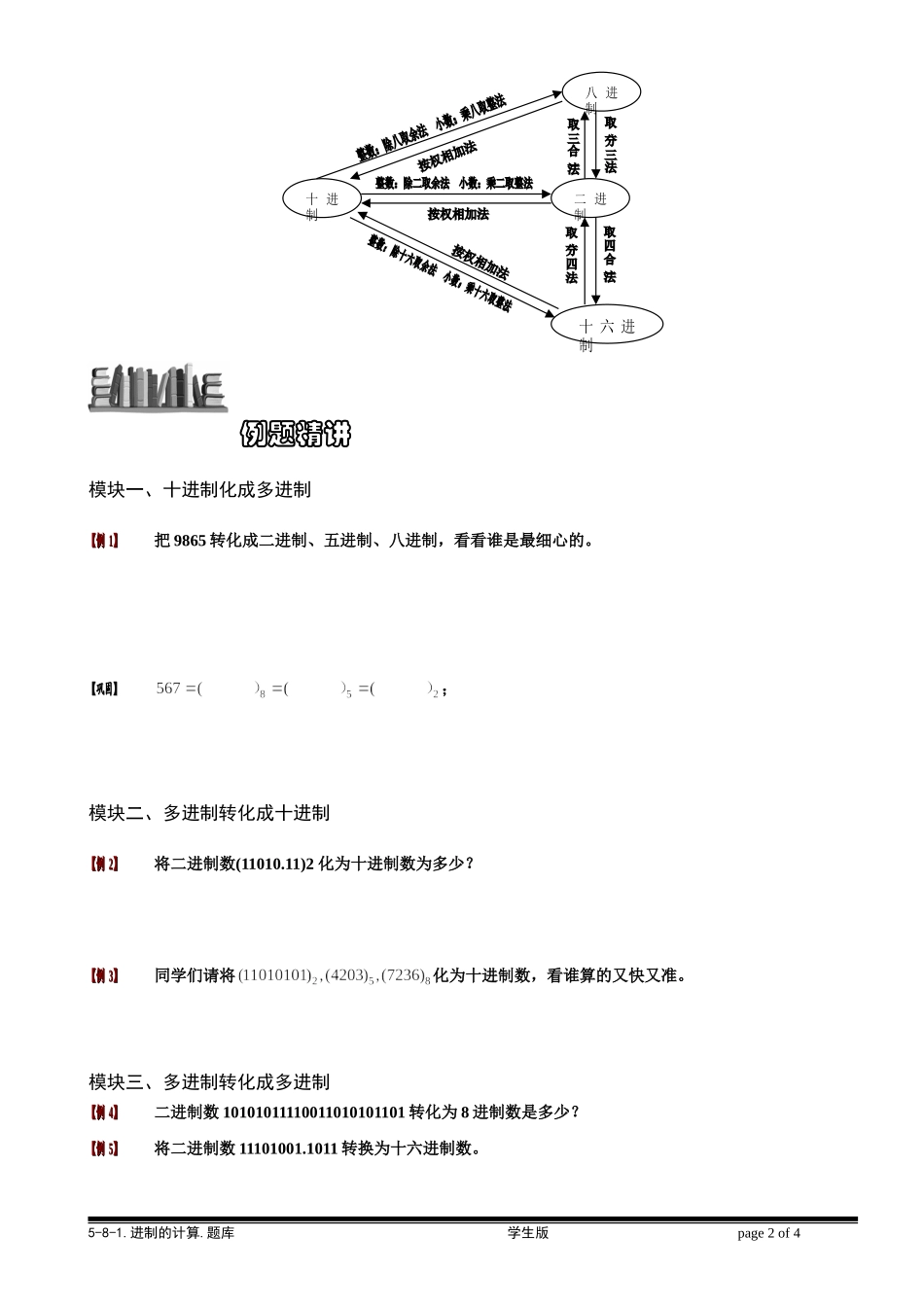
教学目标1.了解进制;2.会将十进制数转换成多进制;3.会将多进制转换成十进制;4.会多进制的混合计算;5.能够判断进制.知识点拨一、数的进制1.十进制:我们常用的进制为十进制,特点是“逢十进一”。在实际生活中,除了十进制计数法外,还有其他的大于1的自然数进位制。比如二进制,八进制,十六进制等。2.二进制:在计算机中,所采用的计数法是二进制,即“逢二进一”。因此,二进制中只用两个数字0和1。二进制的计数单位分别是1、21、22、23、……,二进制数也可以写做展开式的形式,例如100110在二进制中表示为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。注意:对于任意自然数n,我们有n0=1。3.进制:一般地,对于k进位制,每个数是由0,1,2,,共k个数码组成,且“逢k进一”.进位制计数单位是,,,.如二进位制的计数单位是,,,,八进位制的计数单位是,,,.4.进位制数可以写成不同计数单位的数之和的形式十进制表示形式:;二进制表示形式:;为了区别各进位制中的数,在给出数的右下方写上,表示是进位制的数如:,,,分别表示八进位制,二进位制,十二进位制中的数.5.进制的四则混合运算和十进制一样先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。二、进制间的转换:一般地,十进制整数化为进制数的方法是:除以取余数,一直除到被除数小于为止,余数由下到上按从左到右顺序排列即为进制数.反过来,进制数化为十进制数的一般方法是:首先将进制数按的次幂形式展开,然后按十进制数相加即可得结果.如右图所示:5-8-1.进制的计算.题库学生版page1of45-8-1.进制的计算例题精讲模块一、十进制化成多进制【例【例11】】把9865转化成二进制、五进制、八进制,看看谁是最细心的。【巩固】【巩固】;模块二、多进制转化成十进制【例【例22】】将二进制数(11010.11)2化为十进制数为多少?【例【例33】】同学们请将化为十进制数,看谁算的又快又准。模块三、多进制转化成多进制【例【例44】】二进制数10101011110011010101101转化为8进制数是多少?【例【例55】】将二进制数11101001.1011转换为十六进制数。5-8-1.进制的计算.题库学生版page2of4十进制二进制十六进制八进制【例【例66】】某数在三进制中为12120120110110121121,则将其改写为九进制,其从左向右数第位数字是几?模块四、多进制混合计算【例【例77...