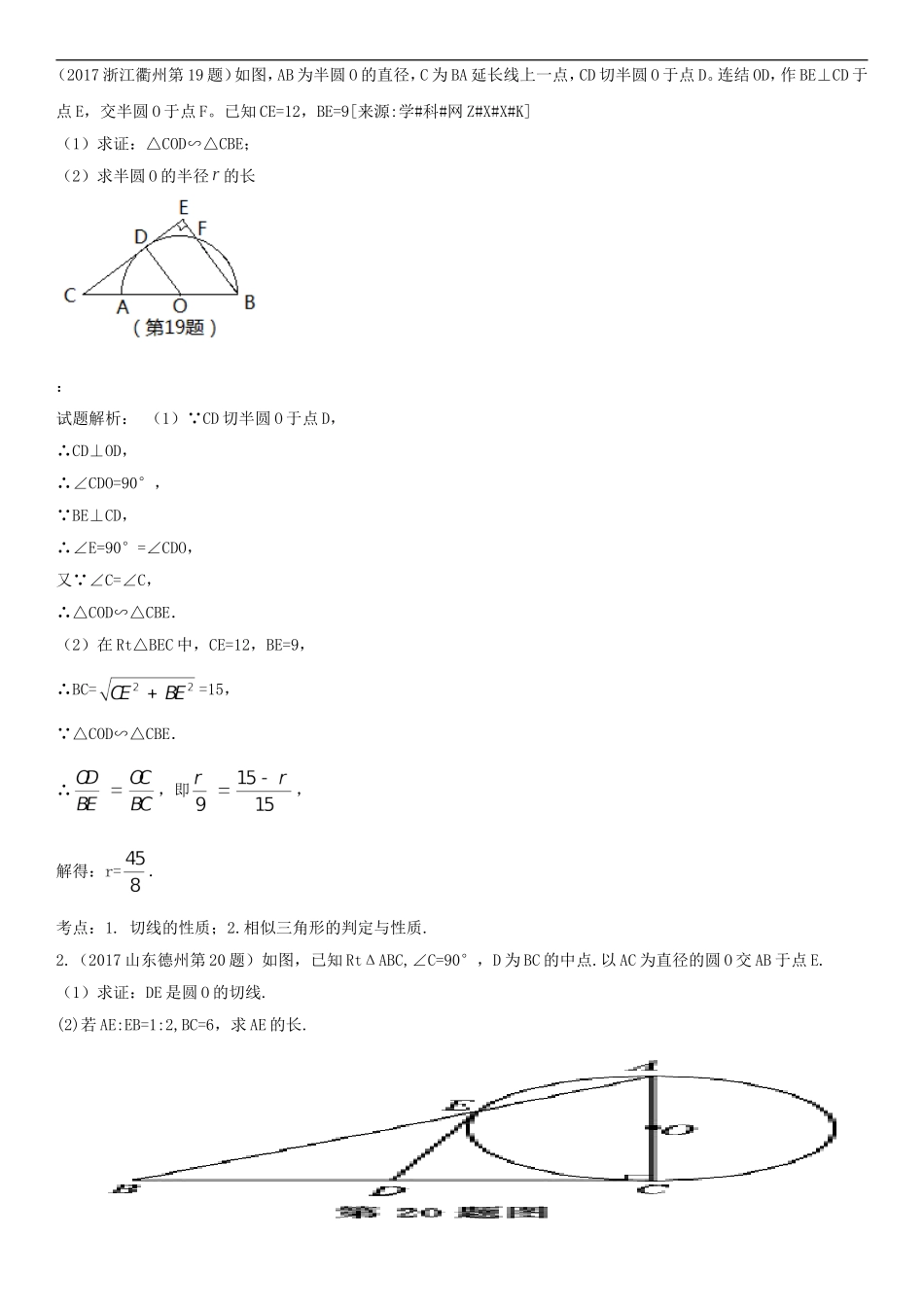
(2017浙江衢州第19题)如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。连结OD,作BE⊥CD于点E,交半圆O于点F。已知CE=12,BE=9[来源:学#科#网Z#X#X#K](1)求证:△COD∽△CBE;(2)求半圆O的半径的长[来源:学#科#网Z#X#X#K]:试题解析:(1) CD切半圆O于点D,∴CD⊥OD,∴∠CDO=90°, BE⊥CD,∴∠E=90°=∠CDO,又 ∠C=∠C,∴△COD∽△CBE.(2)在Rt△BEC中,CE=12,BE=9,∴BC==15, △COD∽△CBE.∴,即,解得:r=.考点:1.切线的性质;2.相似三角形的判定与性质.2.(2017山东德州第20题)如图,已知RtΔABC,∠C=90°,D为BC的中点.以AC为直径的圆O交AB于点E.[来源:Zxxk.Com](1)求证:DE是圆O的切线.(2)若AE:EB=1:2,BC=6,求AE的长.(1)如图所示,连接OE,CE AC是圆O的直径∴∠AEC=∠BEC=90° D是BC的中点∴ED=BC=DC∴∠1=∠2 OE=OC∴∠3=∠4∴∠1+∠3=∠2+∠4,即∠OED=∠ACD ∠ACD=90°∴∠OED=90°,即OE⊥DE又 E是圆O上的一点∴DE是圆O的切线.考点:圆切线判定定理及相似三角形3.(2017甘肃庆阳第27题)如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.(1) A的坐标为(0,6),N(0,2),∴AN=4, ∠ABN=30°,∠ANB=90°,∴AB=2AN=8,∴由勾股定理可知:NB=,∴B(,2).(2)连接MC,NC AN是⊙M的直径,∴∠ACN=90°,∴∠NCB=90°,在Rt△NCB中,D为NB的中点,∴CD=NB=ND,∴∠CND=∠NCD, MC=MN,∴∠MCN=∠MNC, ∠MNC+∠CND=90°,∴∠MCN+∠NCD=90°,即MC⊥CD.∴直线CD是⊙M的切线.考点:切线的判定;坐标与图形性质.4.(2017广西贵港第24题)如图,在菱形中,点在对角线上,且,是的外接圆.(1)求证:是的切线;(2)若求的半径.【答案】(1)证明见解析;(2).(1)连结OP、OA,OP交AD于E,如图, PA=PD,∴弧AP=弧DP,∴OP⊥AD,AE=DE,∴∠1+∠OPA=90°, OP=OA,∴∠OAP=∠OPA,∴∠1+∠OAP=90°, 四边形ABCD为菱形,∴∠1=∠2,∴∠2+∠OAP=90°,∴OA⊥AB,∴直线AB与⊙O相切;(2)连结BD,交AC于点F,如图, 四边形ABCD为菱形,∴DB与AC互相垂直平分, AC=8,tan∠BAC=,∴AF=4,tan∠DAC==,∴DF=2,∴AD==2,∴AE=,在Rt△PAE中,tan∠1==,∴PE=,设⊙O的半径为R,则OE=R﹣,OA=R,在Rt△OAE中, OA2=OE2+AE2,∴R2=(R﹣)2+()2,∴R=,即⊙O的半径...