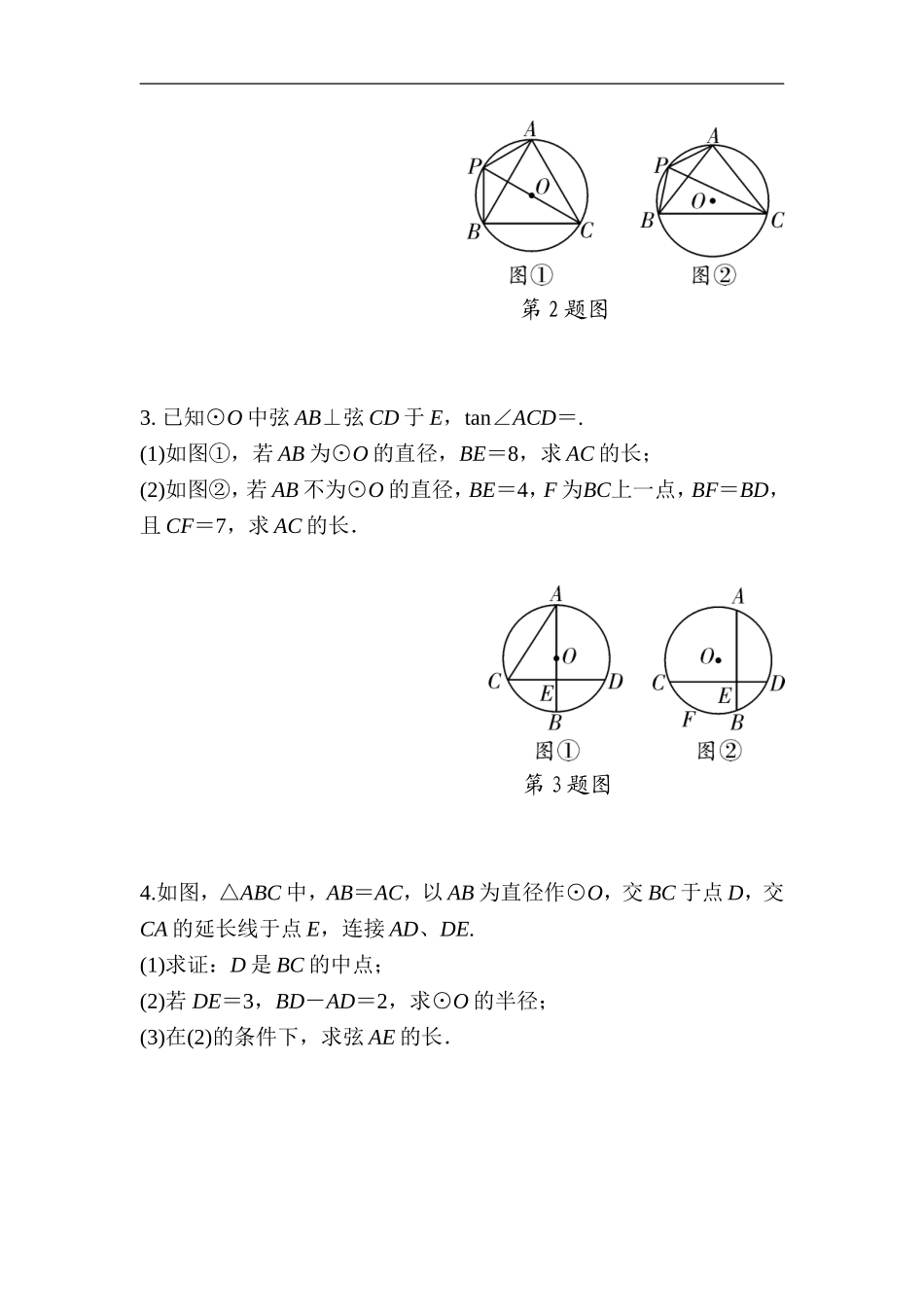
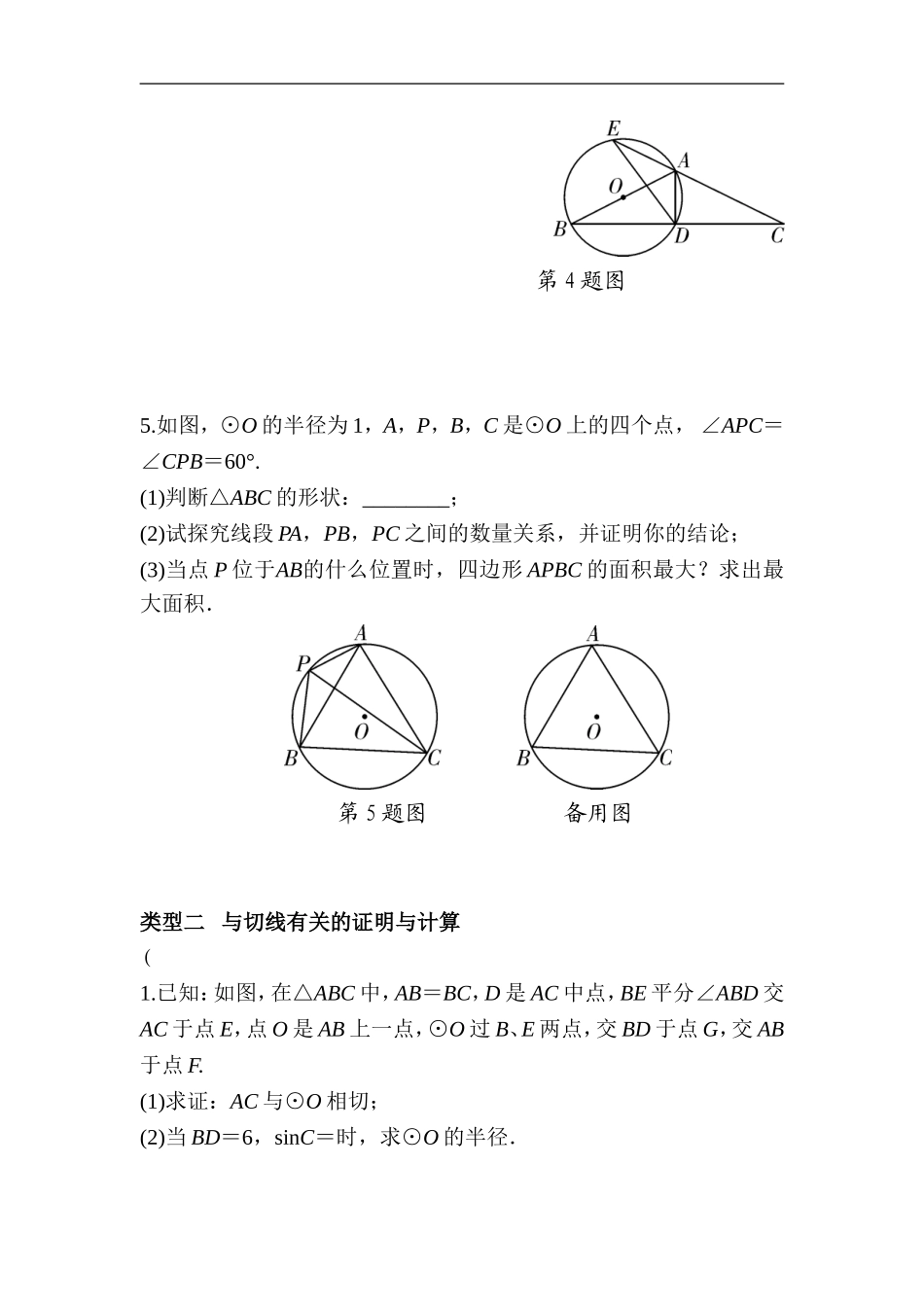
专题二圆的证明与计算类型一圆基本性质的证明与计算1.如图,⊙O的半径为5,点P在⊙O外,PB交⊙O于A、B两点,PC交⊙O于D、C两点.(1)求证:PA·PB=PD·PC;(2)若PA=,AB=,PD=DC+2,求点O到PC的距离.第1题图2.如图,△ABC是⊙O的内接三角形,AB=AC,点P是AB的中点,连接PA,PB,PC.(1)如图①,若∠BPC=60°,求证:AC=AP;(2)如图②,若sin∠BPC=,求tan∠PAB的值.第2题图3.已知⊙O中弦AB⊥弦CD于E,tan∠ACD=.(1)如图①,若AB为⊙O的直径,BE=8,求AC的长;(2)如图②,若AB不为⊙O的直径,BE=4,F为BC上一点,BF=BD,且CF=7,求AC的长.第3题图4.如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.(1)求证:D是BC的中点;(2)若DE=3,BD-AD=2,求⊙O的半径;(3)在(2)的条件下,求弦AE的长.第4题图5.如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.(1)判断△ABC的形状:________;(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;(3)当点P位于AB的什么位置时,四边形APBC的面积最大?求出最大面积.第5题图备用图类型二与切线有关的证明与计算(1.已知:如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.(1)求证:AC与⊙O相切;(2)当BD=6,sinC=时,求⊙O的半径.第1题图2.如图,AB为⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.(1)求证:∠PCA=∠ABC;(2)过点A作AE∥PC,交⊙O于点E,交CD于点F,连接BE.若sin∠P=,CF=5,求BE的长.第2题图3.如图①,在⊙O中,直径AB⊥CD于点E,点P在BA的延长线上,且满足∠PDA=∠ADC.(1)判断直线PD与⊙O的位置关系,并说明理由;(2)延长DO交⊙O于M(如图②),当M恰为BC的中点时,试求的值;(3)若PA=2,tan∠PDA=,求⊙O的半径.第3题图1.如图,在Rt△ABC中,∠ACB=90°,E是BC的中点,以AC为直径的⊙O与AB边交于点D,连接DE.(1)求证:△ABC∽△CBD;(2)求证:直线DE是⊙O的切线.第1题图2.如图,⊙O的圆心在Rt△ABC的直角边AC上,⊙O经过C、D两点,与斜边AB交于点E,连接BO、ED,有BO∥ED,作弦EF⊥AC于G,连接DF.(1)求证:CO·CD=DE·BO;(2)若⊙O的半径为5,sin∠DFE=,求EF的长.第2题图3.如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.(1)求...