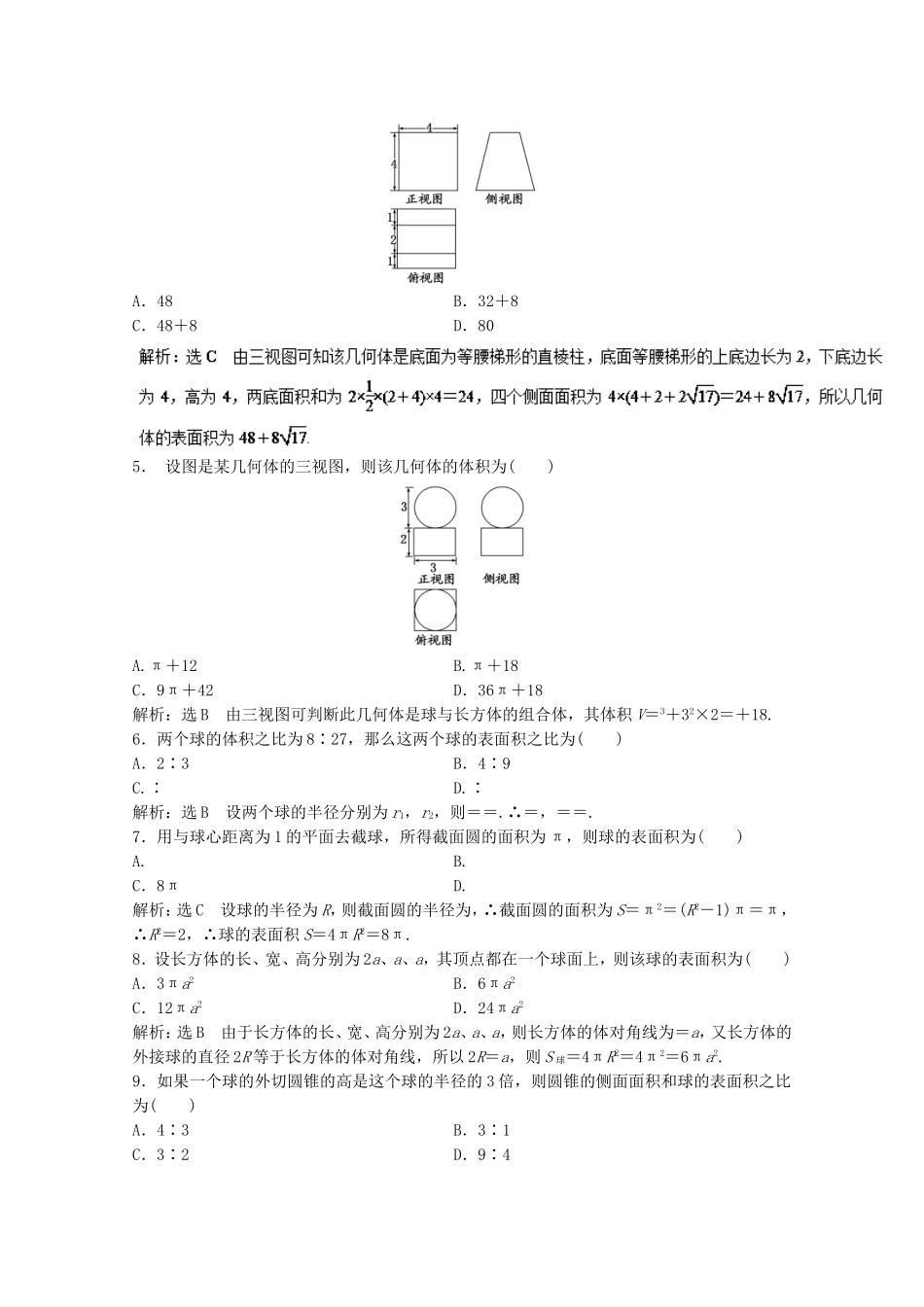
(测试时间:120分钟满分:150分)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图,ABC-A′B′C′是体积为1的棱柱,则四棱锥C-AA′B′B的体积是()A.B.C.D.解析:选C VC-A′B′C′=V柱=,∴VC-AA′B′B=1-=.2.如果轴截面为正方形的圆柱的侧面积是4π,那么圆柱的体积等于()A.πB.2πC.4πD.8π3.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为()A.6B.9C.12D.18解析:选B由三视图可知该几何体为底面是斜边为6的等腰直角三角形,高为3的三棱锥,其体积为××6×3×3=9.4.一个空间几何体的三视图如图所示,则该几何体的表面积为()A.48B.32+8C.48+8D.805.设图是某几何体的三视图,则该几何体的体积为()A.π+12B.π+18C.9π+42D.36π+18解析:选B由三视图可判断此几何体是球与长方体的组合体,其体积V=3+32×2=+18.6.两个球的体积之比为8∶27,那么这两个球的表面积之比为()A.2∶3B.4∶9C.∶D.∶解析:选B设两个球的半径分别为r1,r2,则==.∴=,==.7.用与球心距离为1的平面去截球,所得截面圆的面积为π,则球的表面积为()A.B.C.8πD.解析:选C设球的半径为R,则截面圆的半径为,∴截面圆的面积为S=π2=(R2-1)π=π,∴R2=2,∴球的表面积S=4πR2=8π.8.设长方体的长、宽、高分别为2a、a、a,其顶点都在一个球面上,则该球的表面积为()A.3πa2B.6πa2C.12πa2D.24πa2解析:选B由于长方体的长、宽、高分别为2a、a、a,则长方体的体对角线为=a,又长方体的外接球的直径2R等于长方体的体对角线,所以2R=a,则S球=4πR2=4π2=6πa2.9.如果一个球的外切圆锥的高是这个球的半径的3倍,则圆锥的侧面面积和球的表面积之比为()A.4∶3B.3∶1C.3∶2D.9∶4解析:选C作轴截面如图,则PO=2OD,∠CPB=30°,CB=PC=r,PB=2r,圆锥侧面积S1=6πr2,球的面积S2=4πr2,S1∶S2=3∶2.10.平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为()A.πB.4πC.4πD.6π11.已知长方体的长、宽、高分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是()A.25πB.50πC.125πD.都不对B由题意知球为长方体的外接球.设球的半径为R,则(2R)2=32+42+52,∴R2=,∴S球=4πR2=4π×=50π.12.一个空间几何体的三视图如图L135所示...