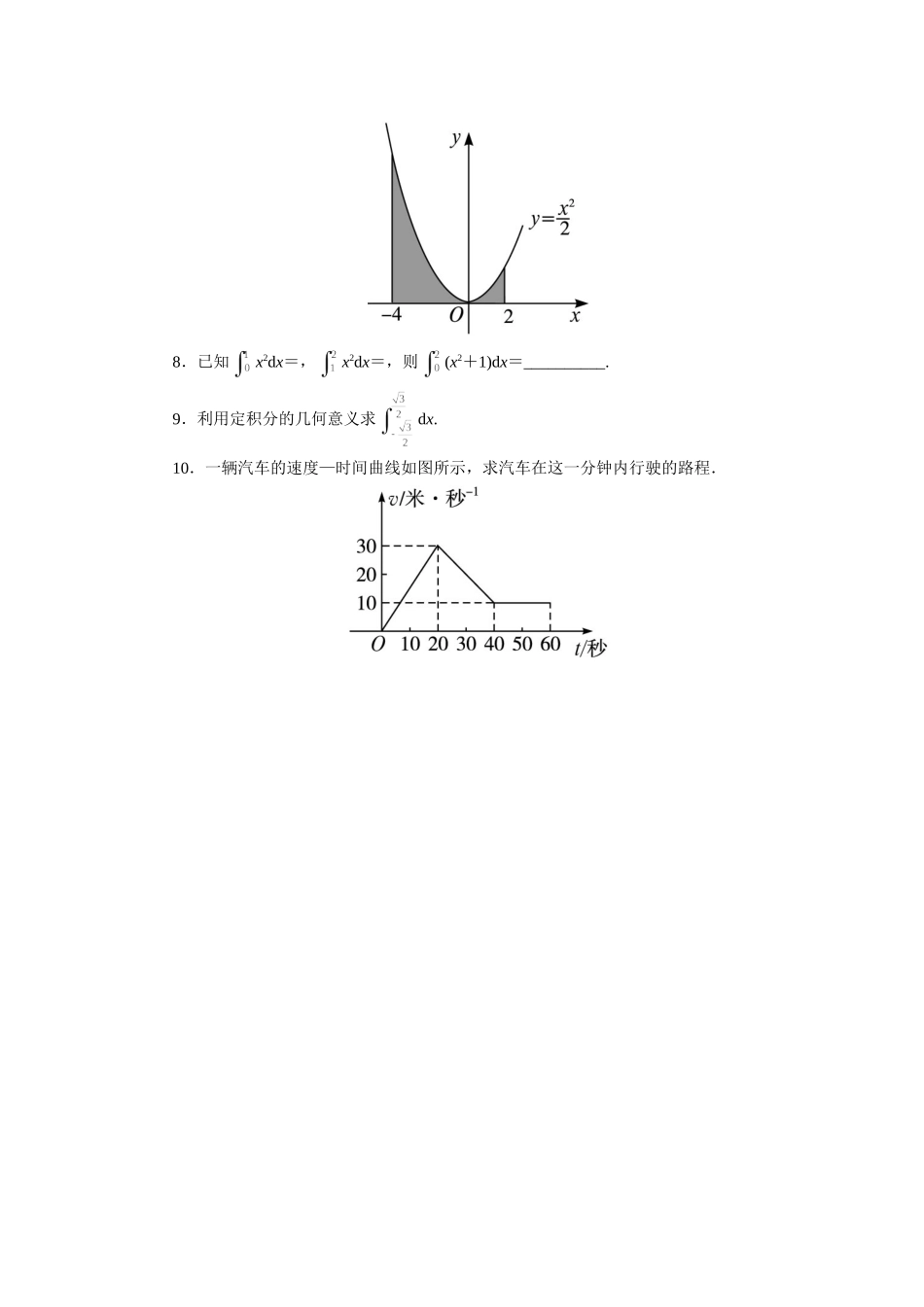
自我小测1.下列结论中成立的个数是()①x3dx=·;②x3dx=lim·;③x3dx=lim·.A.0B.1C.2D.32.如图所示,阴影部分的面积为()A.f(x)dxB.g(x)dxC.[f(x)-g(x)]dxD.[g(x)-f(x)]dx3.由定积分的几何意义可得2xdx=()A.6B.16C.25D.344.下列等式成立的是()A.xdx=2B.(-x)dx=C.|x|dx=2|x|dxD.2dx=05.定积分xdx与dx的大小关系是()A.xdx<dxB.xdx>dxC.xdx≥dxD.无法确定6.计算(-2016)dx=__________.7.如图所示阴影部分的面积用定积分表示为__________.8.已知x2dx=,x2dx=,则(x2+1)dx=__________.9.利用定积分的几何意义求dx.10.一辆汽车的速度—时间曲线如图所示,求汽车在这一分钟内行驶的路程.参考答案1.解析:由定积分的定义,易知②③正确,①错误,故选C.答案:C2.解析:由题图可知,当x∈[a,b]时,f(x)>g(x),所以阴影部分的面积S=f(x)dx-g(x)dx=[f(x)-g(x)]dx.答案:C3.解析:2xdx的值表示由直线y=2x,x=3,x=5,y=0所围成图形的面积S=×(6+10)×2=16.答案:B4.解析:∵xdx=,(-x)dx=-,2dx=4,∴A,B,D不正确.∵函数y=|x|为偶函数,∴|x|dx=2|x|dx,∴C正确.答案:C5.解析:由定积分的几何意义结合下图可知xdx<dx.答案:A6.解析:∵根据定积分的几何意义,2016dx表示直线x=2014,x=2015,y=0,y=2016围成的矩形面积,∴2016dx=2016.∴(-2016)dx=2016dx=-2016.答案:-20167.解析:阴影部分由直线x=-4,x=2,y=0和曲线y=围成,所以由定积分的几何意义可知阴影部分的面积用定积分表示为dx.答案:dx8.解析:由定积分的性质,可得(x2+1)dx=x2dx+1dx,而由已知,有x2dx=x2dx+x2dx=+=,又由定积分的几何意义知1dx=1×2=2,故(x2+1)dx=+2=.答案:9.解:由可知,x2+y2=1(y≥0)的图象为如图所示的半圆,由定积分的几何意义知等于圆心角为120°的弓形CED的面积与矩形ABCD的面积之和.S弓形=,S矩形=|AB|·|BC|=,∴.10.解:由题意,汽车的速度v与时间t的函数关系式为v(t)=所以该汽车在这一分钟内所行驶的路程为s=v(t)dt=tdt+(50-t)dt+10dt=300+400+200=900(米).