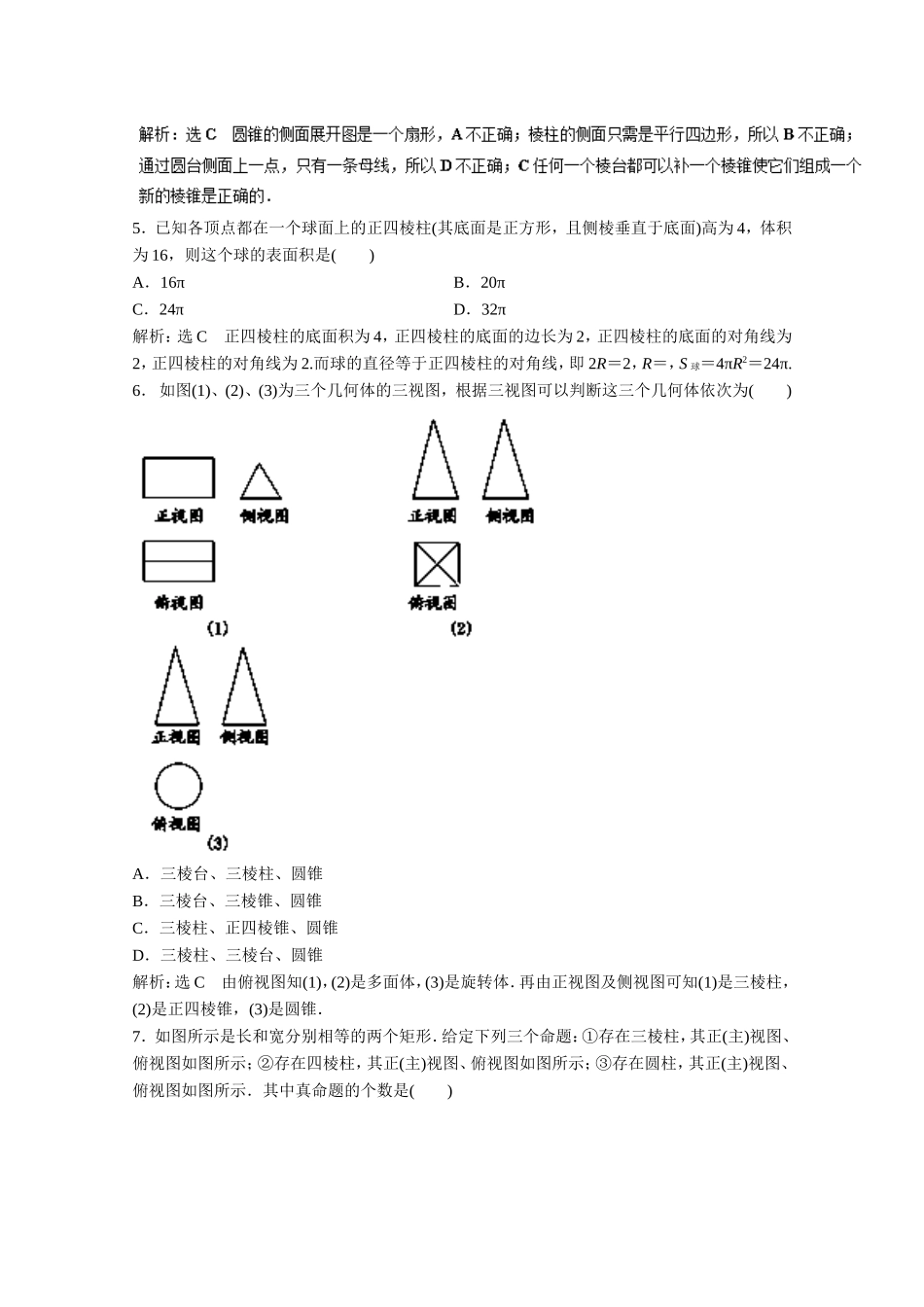
(测试时间:120分钟满分:150分)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列命题中,正确的是()A.有两个侧面是矩形的棱柱是直棱柱B.侧面都是等腰三角形的棱锥是正棱锥C.侧面都是矩形的直四棱柱是长方体D.底面为正多边形,且有相邻两个侧面与底面垂直的棱柱是正棱柱解析:选D认识棱柱一般要从侧棱与底面的垂直与否和底面多边形的形状两方面去分析,故A,C都不够准确,B中对等腰三角形的腰是否为侧棱未作说明,故也不正确.2.如图所示,观察四个几何体,其中判断正确的是()A.(1)是棱台B.(2)是圆台C.(3)是棱锥D.(4)不是棱柱3.如图所示的直观图的平面图形ABCD是()A.任意梯形B.直角梯形C.任意四边形D.平行四边形解析:选BAB∥Oy,AD∥Ox,故AB⊥AD.又BC∥AD且BC≠AD,所以为直角梯形.4.下列说法正确的是()A.圆锥的侧面展开图是一个等腰三角形B.棱柱即是两个底面全等且其余各面都是矩形的多面体C.任何一个棱台都可以补一个棱锥使它们组成一个新的棱锥D.通过圆台侧面上一点,有无数条母线5.已知各顶点都在一个球面上的正四棱柱(其底面是正方形,且侧棱垂直于底面)高为4,体积为16,则这个球的表面积是()A.16πB.20πC.24πD.32π解析:选C正四棱柱的底面积为4,正四棱柱的底面的边长为2,正四棱柱的底面的对角线为2,正四棱柱的对角线为2.而球的直径等于正四棱柱的对角线,即2R=2,R=,S球=4πR2=24π.6.如图(1)、(2)、(3)为三个几何体的三视图,根据三视图可以判断这三个几何体依次为()A.三棱台、三棱柱、圆锥B.三棱台、三棱锥、圆锥C.三棱柱、正四棱锥、圆锥D.三棱柱、三棱台、圆锥解析:选C由俯视图知(1),(2)是多面体,(3)是旋转体.再由正视图及侧视图可知(1)是三棱柱,(2)是正四棱锥,(3)是圆锥.7.如图所示是长和宽分别相等的两个矩形.给定下列三个命题:①存在三棱柱,其正(主)视图、俯视图如图所示;②存在四棱柱,其正(主)视图、俯视图如图所示;③存在圆柱,其正(主)视图、俯视图如图所示.其中真命题的个数是()A.3B.2C.1D.0解析:选A只需①底面是等腰直角三角形的直三棱柱,让其直角三角形的直角边所在的一个侧面平卧;②正四棱柱平躺;③圆柱平躺即可使得三个命题为真.8.如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积是()A.6B.3C.6D.129.轴截面为正方形的圆柱的侧面积与全面积的比是()A.1∶...