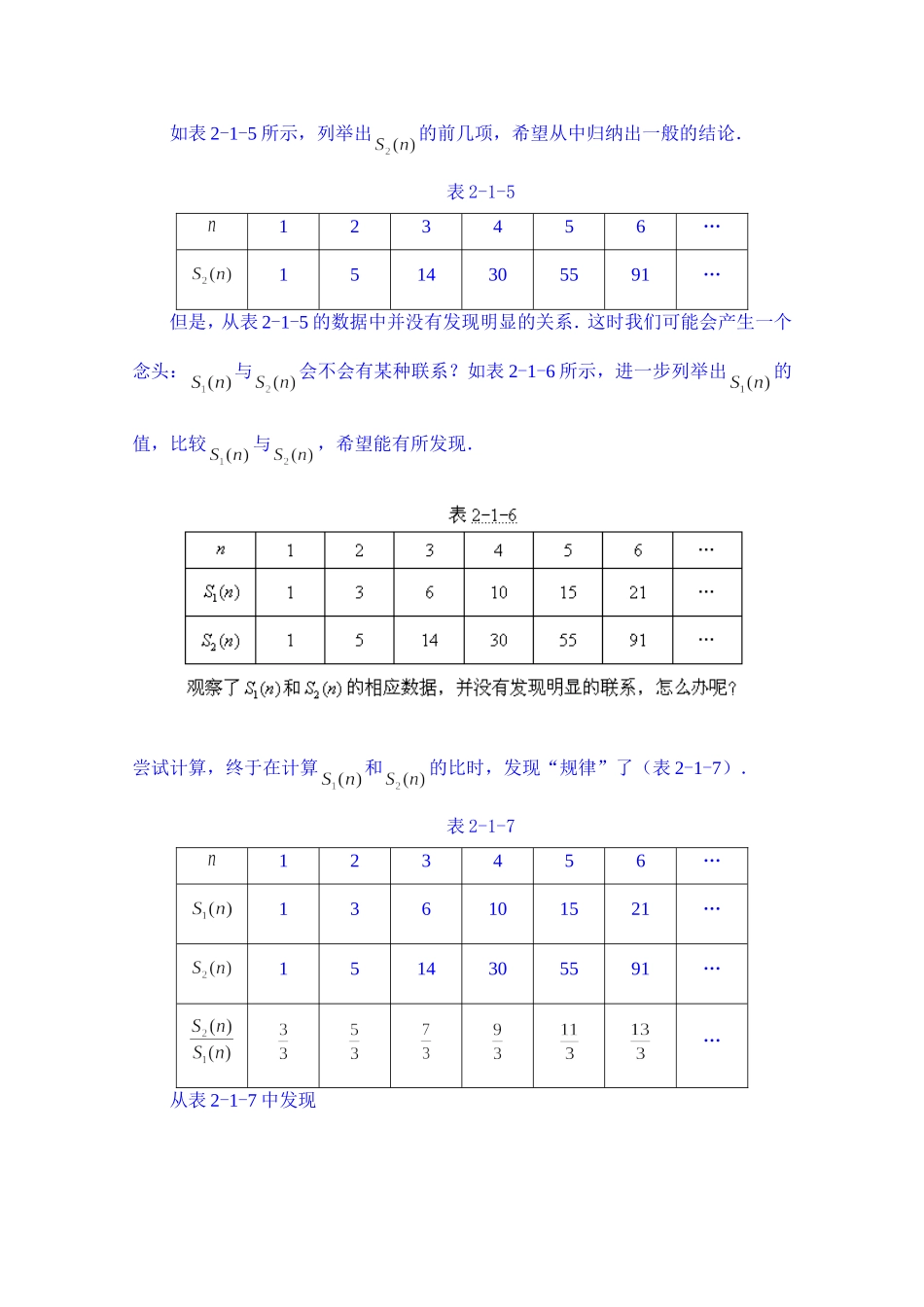
教学目标:1.了解合情推理和演绎推理的含义.2.能正确地运用合情推理和演绎推理进行简单的推理.3.了解合情推理与演绎推理之间的联系与差别.教学重点:了解合情推理与演绎推理之间的联系与差别.教学难点:了解合情推理和演绎推理是怎样推进数学发现活动的.教学过程:一、知识回顾从一个或几个已知命题得出另一个新命题的思维过程称为推理.合情推理和演绎推理之间具有怎样的联系和差异?合情推理和演绎推理是怎样推进数学发现活动的?三个推理案例的共同点是它们都是由“前提”和“结论”两部分组成,但是在推理的结构形式上表现出不同的特点,据此可以分为合情推理与演绎推理.二、数学运用例1正整数平方和公式的推导.分析提出问题:我们知道,前个正整数的和为①那么,前个正整数的和?②数学活动思路1(归纳的方案)如表2-1-5所示,列举出的前几项,希望从中归纳出一般的结论.表2-1-5123456…1514305591…但是,从表2-1-5的数据中并没有发现明显的关系.这时我们可能会产生一个念头:与会不会有某种联系?如表2-1-6所示,进一步列举出的值,比较与,希望能有所发现.尝试计算,终于在计算和的比时,发现“规律”了(表2-1-7).表2-1-7123456…136101521…1514305591……从表2-1-7中发现,于是,猜想.公式③的正确性还需要证明.思考上面的数学活动是由哪些环节构成的?在这个过程中提出了哪些猜想?提出猜想时使用了哪些推理方法?合情推理和演绎推理分别发挥什么作用?思路2(演绎的方案)尝试用直接相加的方法求出正整数的平方和.(1)把正整数的平方表示出来,有12=1,22=,32=,42=,…n2=,左右两边分别相加,得,等号两边的被消去了,所以无法从中求出的值,尝试失败了!(2)从失败中汲取有用信息,进行新的尝试.前面的失败尝试还是有意义的,因为尽管我们没有求出,但是却求出了的表达式,即.它启示我们:既然能用上面的方法求出,那么我们也应该可以用类似的方法求出.(3)尝试把两项和的平方公式改为两项和的立方公式.具体方法如下:13=1,23=,33=,43=,…43=.左右两边分别相加,得.由此可知==,终于导出了公式.思考上面的数学活动是由哪些环节构成的?在这个过程中提出了哪些猜想?提出猜想时使用了哪些推理方法?合情推理和演绎推理分别发挥了什么作用?例2棱台体积公式的推导.提出问题能通过类比推测出棱台的体积公式吗?数学活动思路:试图以四棱台为例,通过和梯形的类比推测公式.(1)确定类...