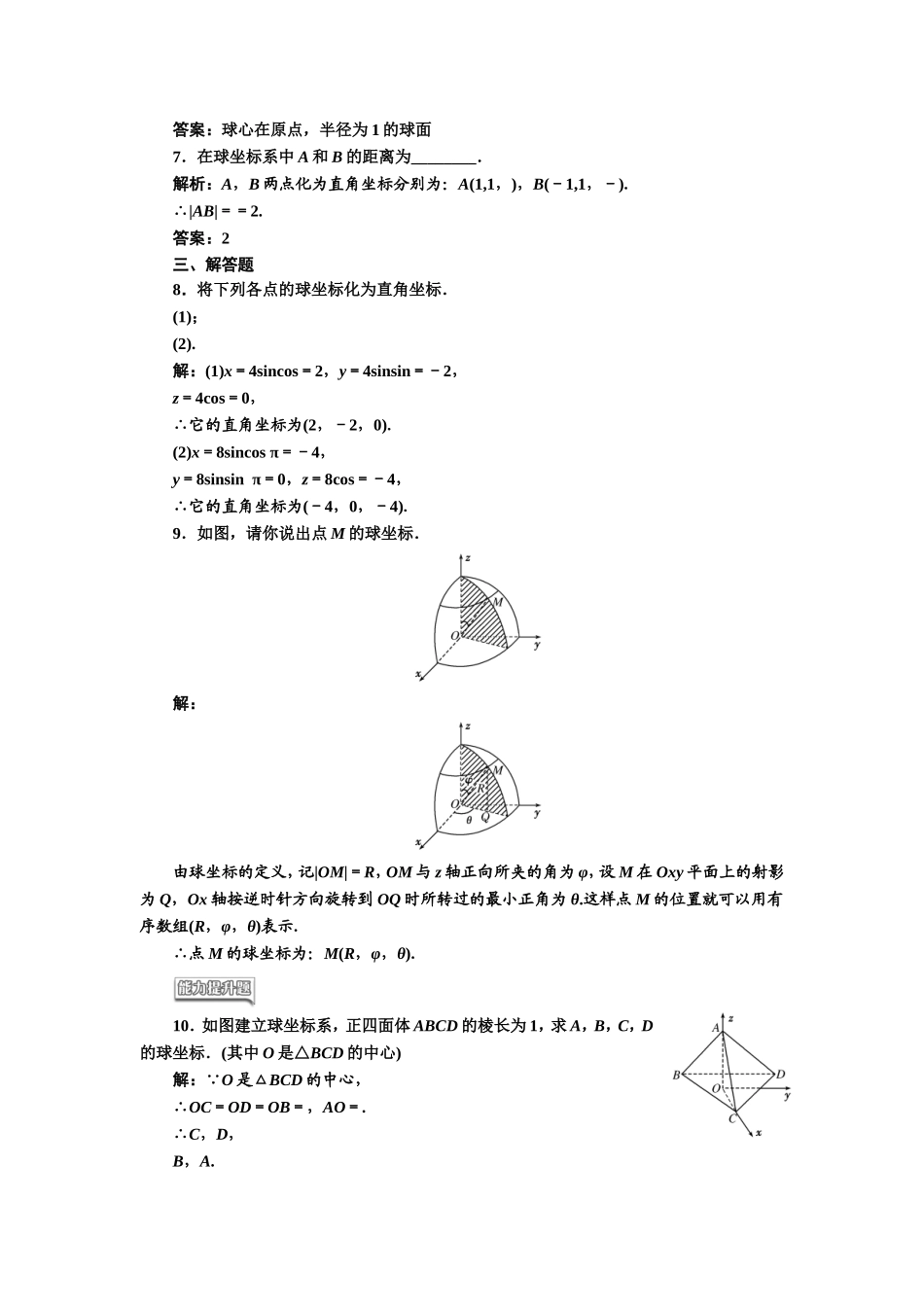
课时跟踪检测(六)球坐标系一、选择题1.已知一个点的球坐标为,则它的方位角为()A.B.C.D.解析:选A由球坐标的定义可知选A.2.设点M的柱坐标为,则它的球坐标为()A.B.C.D.解析:选B设点M的直角坐标为(x,y,z),故设点M的球坐标为(ρ,φ,θ).则ρ==2,由=2cosφ知φ=.又tanθ==1,故θ=,故点M的球坐标为.3.点P的球坐标为,则它的直角坐标为()A.(1,0,0)B.(-1,-1,0)C.(0,-1,0)D.(-1,0,0)解析:选Dx=rsinφcosθ=1·sin·cosπ=-1,y=rsinφsinθ=1·sin·sinπ=0,z=rcosφ=1·cos=0.∴它的直角坐标为(-1,0,0).4.设点M的直角坐标为(-1,-1,),则它的球坐标为()A.B.C.D.解析:选B由坐标变换公式,得r==2,cosφ==,∴φ=.∵tanθ===1,∴θ=.∴M的球坐标为.二、填空题5.已知点M的球坐标为,则它的直角坐标为________,它的柱坐标是________.解析:由坐标变换公式直接得直角坐标和柱坐标.答案:(-2,2,2)6.在球坐标系中,方程r=1表示________.解析:数形结合,根据球坐标的定义判断形状.答案:球心在原点,半径为1的球面7.在球坐标系中A和B的距离为________.解析:A,B两点化为直角坐标分别为:A(1,1,),B(-1,1,-).∴|AB|==2.答案:2三、解答题8.将下列各点的球坐标化为直角坐标.(1);(2).解:(1)x=4sincos=2,y=4sinsin=-2,z=4cos=0,∴它的直角坐标为(2,-2,0).(2)x=8sincosπ=-4,y=8sinsinπ=0,z=8cos=-4,∴它的直角坐标为(-4,0,-4).9.如图,请你说出点M的球坐标.解:由球坐标的定义,记|OM|=R,OM与z轴正向所夹的角为φ,设M在Oxy平面上的射影为Q,Ox轴按逆时针方向旋转到OQ时所转过的最小正角为θ.这样点M的位置就可以用有序数组(R,φ,θ)表示.∴点M的球坐标为:M(R,φ,θ).10.如图建立球坐标系,正四面体ABCD的棱长为1,求A,B,C,D的球坐标.(其中O是△BCD的中心)解:∵O是△BCD的中心,∴OC=OD=OB=,AO=.∴C,D,B,A.